F Distribution in R (4 Examples) | df, pf, qf & rf Functions
In this article, I’ll illustrate how to apply the F distribution functions in the R programming language.
The tutorial will contain this:
- Example 1: F Density in R (df Function)
- Example 2: F Cumulative Distribution Function (pf Function)
- Example 3: F Quantile Function (qf Function)
- Example 4: Simulation of Random Numbers (rf Function)
- Video, Further Resources & Summary
Let’s take a look at some R codes in action…
Example 1: F Density in R (df Function)
In the first example of this tutorial, I’ll explain how to draw a density plot of the F distribution. As a first step, we need to create some input data for the df R function:
x_df <- seq(0, 20, by = 0.1) # Specify x-values for df function
Now, we can apply the df command to this data…
y_df <- df(x_df, df1 = 3, df2 = 5) # Apply df function
…and use the R plot function to create a graph representing the F density:
plot(y_df) # Plot df values
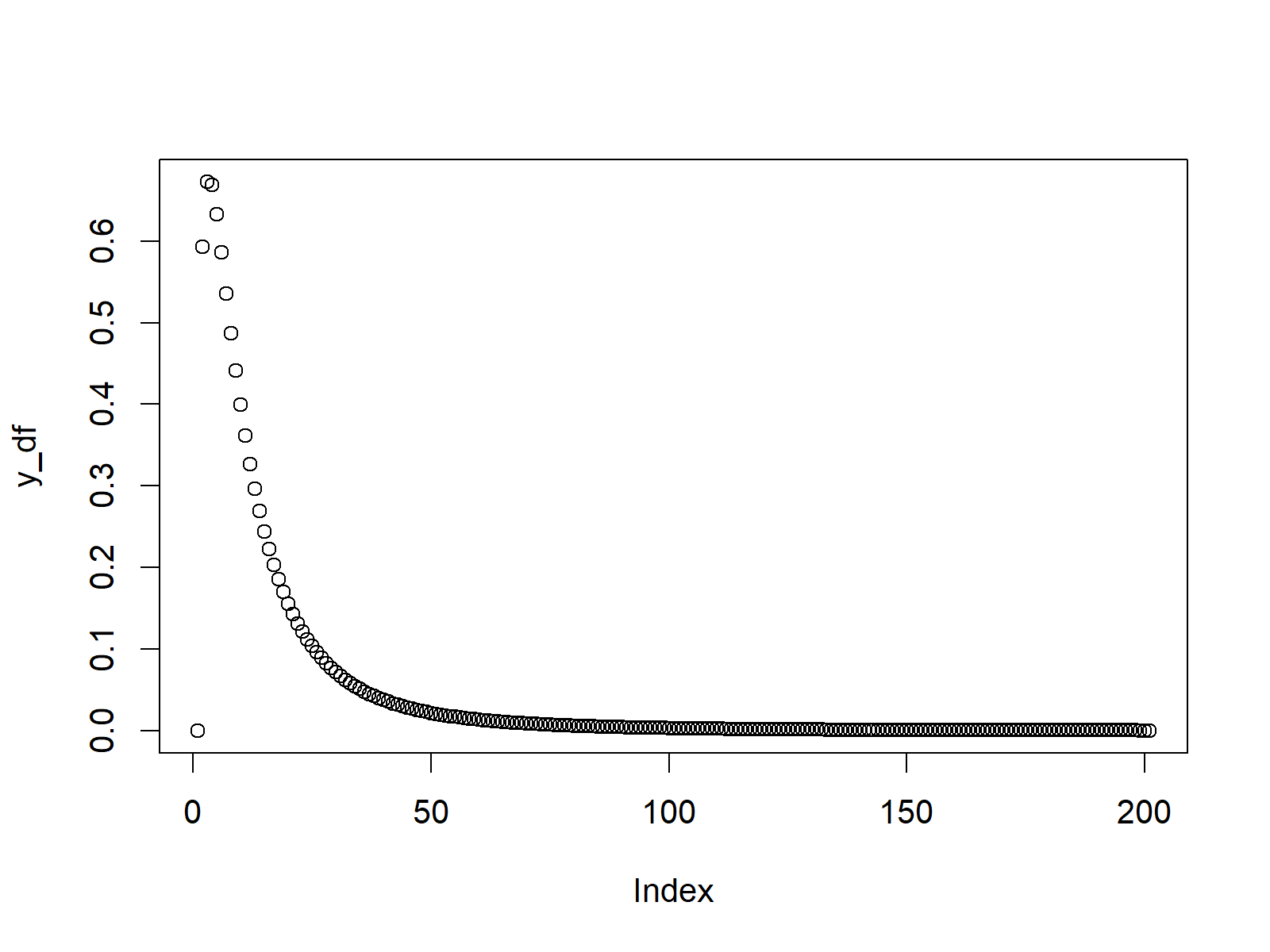
Figure 1: Density of F Distribution.
Example 2: F Cumulative Distribution Function (pf Function)
In the second example, you’ll learn how to draw a cumulative distribution function (CDF) of the F distribution. First, we have to create a vector of quantiles as input:
x_pf <- seq(0, 20, by = 0.1) # Specify x-values for pf function
Now, we can apply the pf function to this input vector:
y_pf <- pf(x_pf, df1 = 3, df2 = 5) # Apply pf function
We can draw a plot of the output of the pf function as shown below:
plot(y_pf) # Plot pf values
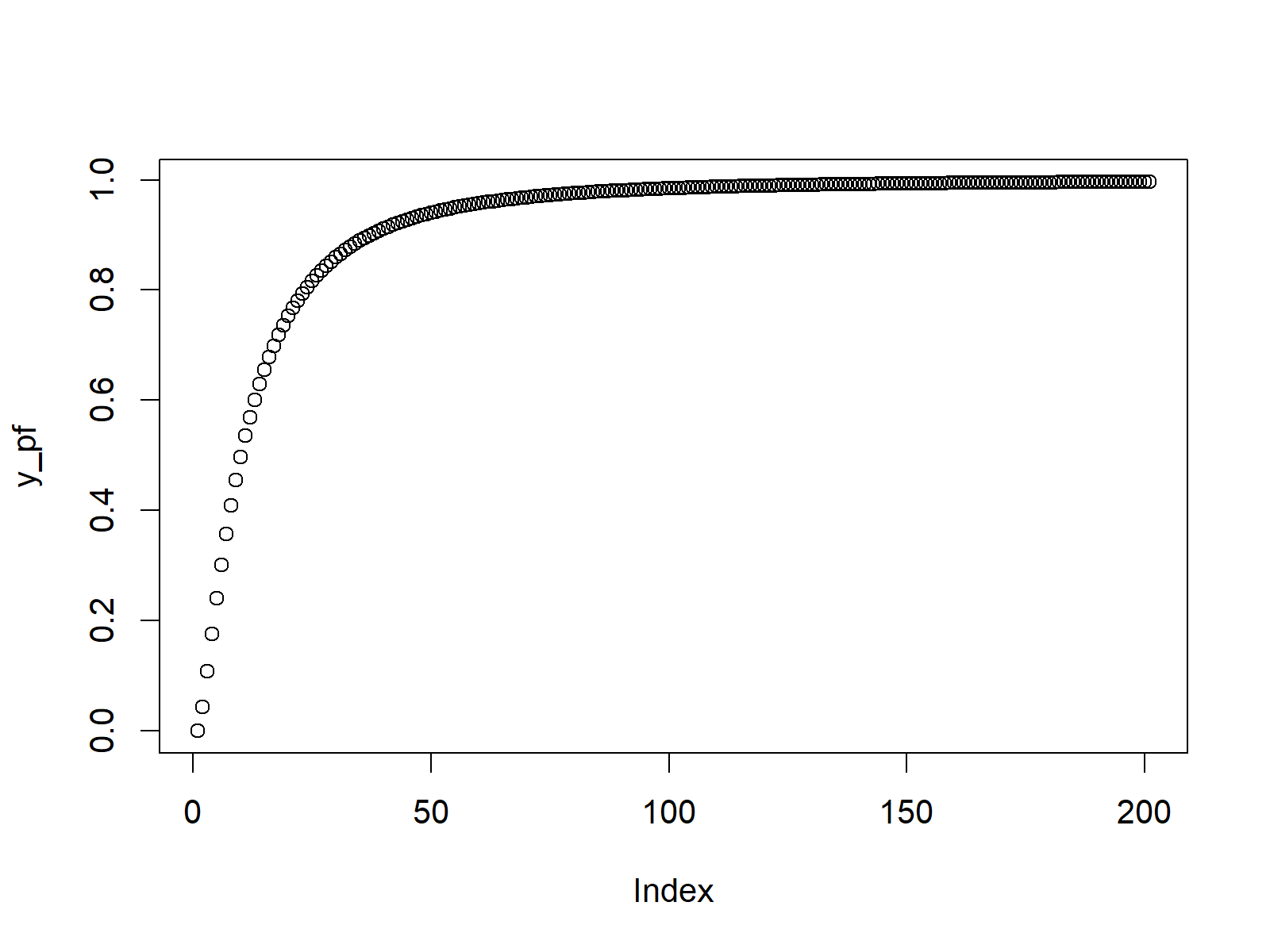
Figure 2: Cumulative Distribution Function of F Distribution.
Example 3: F Quantile Function (qf Function)
In the next example, we’ll draw a quantile function plot of the F distribution. First, we need to create a sequence of probabilities:
x_qf <- seq(0, 1, by = 0.01) # Specify x-values for qf function
Then, we can apply the qf function in order to get the corresponding quantile function values for our input sequence:
y_qf <- qf(x_qf, df1 = 3, df2 = 5) # Apply qf function
And finally, we can draw a plot:
plot(y_qf) # Plot qf values
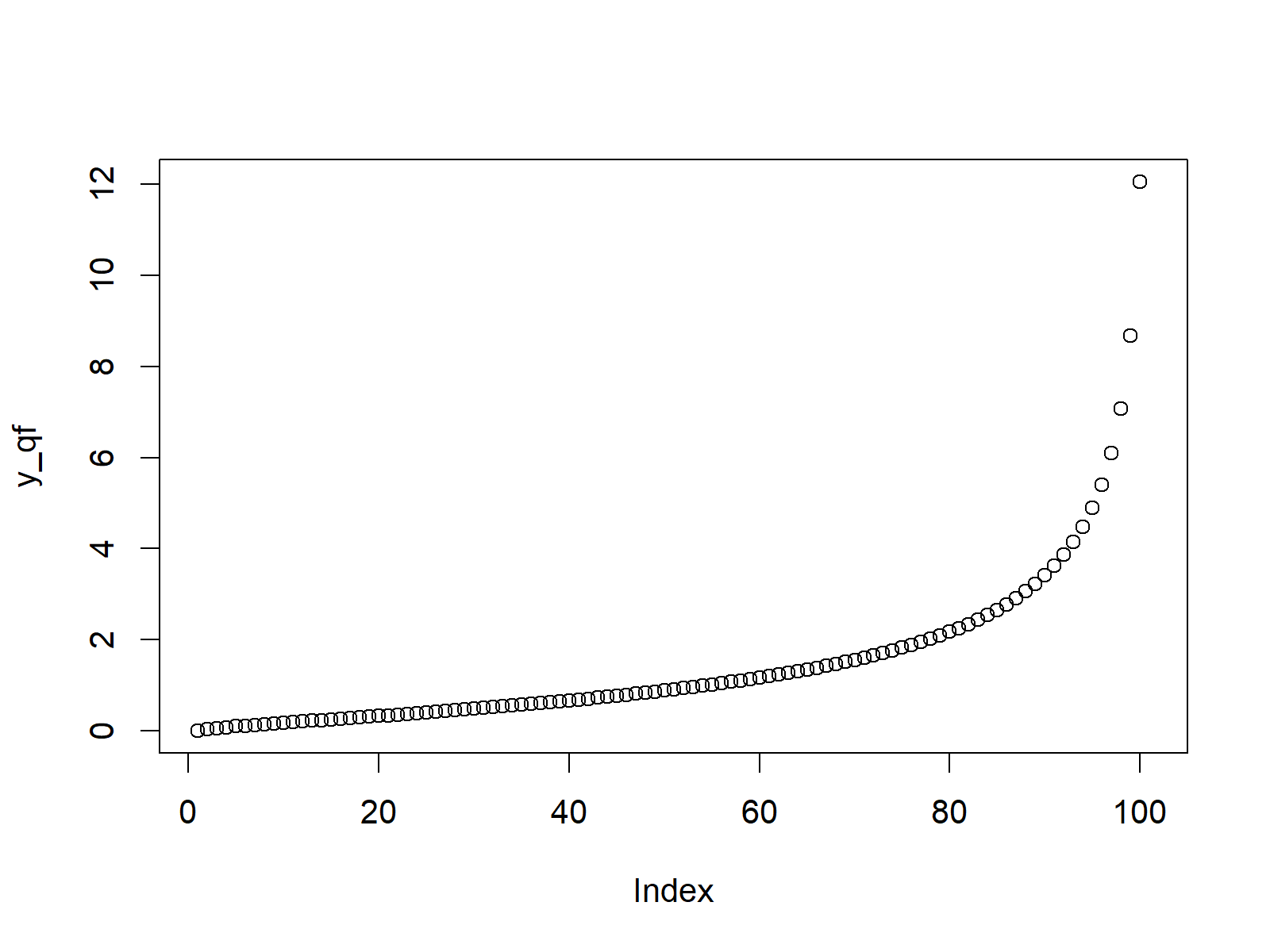
Figure 3: Quantile Function of F Distribution.
Example 4: Simulation of Random Numbers (rf Function)
To generate a set of random numbers, we need to specify a seed and a sample size:
set.seed(53535) # Set seed for reproducibility N <- 10000 # Specify sample size
Then, we can use the rf function to draw random numbers according to the F distribution:
y_rf <- rf(N, df1 = 3, df2 = 5) # Draw N F-distributed values y_rf # Print values to RStudio console # 0.419950200 1.089996596 0.334007814 0.069551464 0.367587034 1.386032672 0.531977959 0.772345591 1.587337077
The output of the RStudio console illustrates the values created by the rf command. We can now plot these random numbers in a histogram as follows:
hist(y_rf, # Plot of randomly drawn f density breaks = 500, main = "", xlim = c(0, 15))
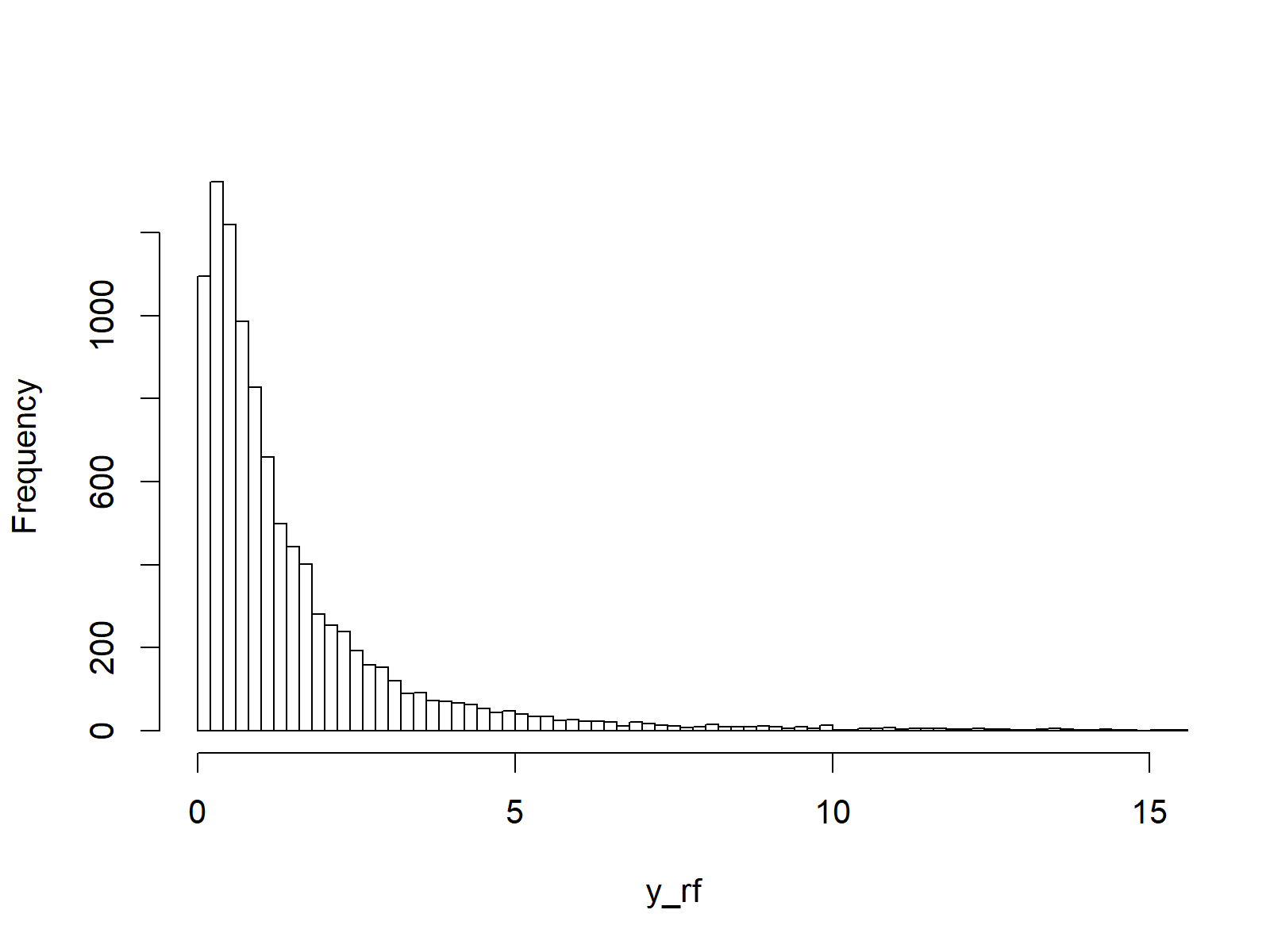
Figure 4: Random Numbers Generated According to F Distribution.
Video, Further Resources & Summary
I have recently published a video on the Statistics Globe YouTube channel, which shows the R programming code of this article. You can find the video below:
The YouTube video will be added soon.
You could also have a look at the other articles on probability distributions and the simulation of random numbers in R:
- Bernoulli Distribution in R
- Beta Distribution in R
- Binomial Distribution in R
- Bivariate & Multivariate Distributions in R
- Cauchy Distribution in R
- Chi-Squred Distribution in R
- Exponential Distribution in R
- F Distribution in R
- Gamma Distribution in R
- Geometric Distribution in R
- Hypergeometric Distribution in R
- Log Normal Distribution in R
- Logistic Distribution in R
- Negative Binomial Distribution in R
- Normal Distribution in R
- Poisson Distribution in R
- Student t Distribution in R
- Studentized Range Distribution in R
- Uniform Distribution in R
- Weibull Distribution in R
- Wilcoxon Signedank Statistic Distribution in R
- Wilcoxonank Sum Statistic Distribution in R
In addition, you may read some of the other articles on my homepage. A selection of tutorials can be found here.
Summary: At this point you should have learned how to use the F functions in the R programming language. Let me know in the comments, if you have any additional questions. Furthermore, don’t forget to subscribe to my email newsletter in order to receive regular updates on new tutorials.






