Statistics Globe

Probability Distributions in R (Examples) | PDF, CDF & Quantile Function

 

This page explains the functions for different probability distributions provided by the R programming language.

In general, R provides programming commands for the probability distribution function (PDF), the cumulative distribution function (CDF), the quantile function, and the simulation of random numbers according to the probability distributions.

The naming of the different R commands follows a clear structure. See the table below for the names of all R functions:

 

all probability distribution functions of the r programming language

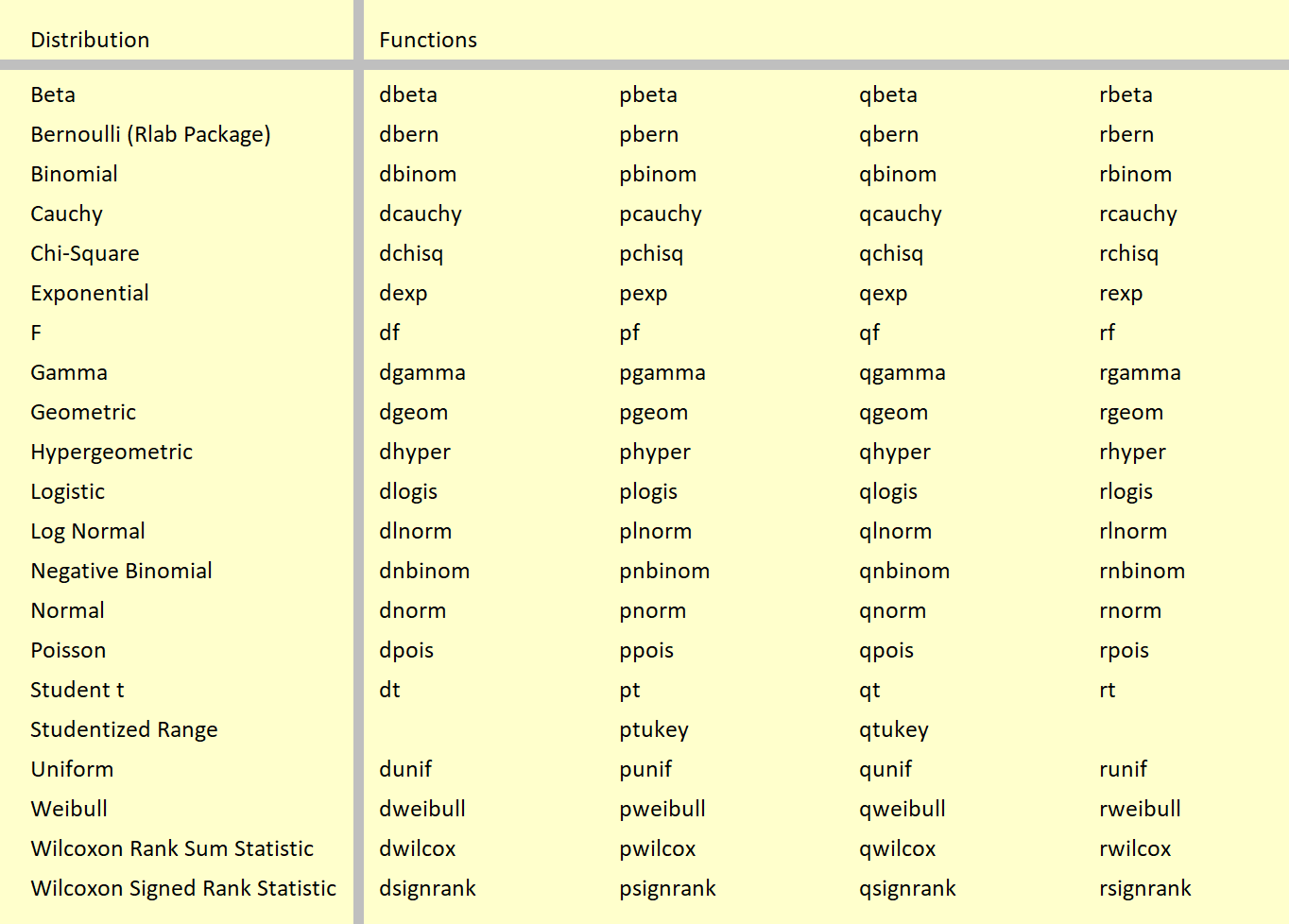
Table 1: The Probability Distribution Functions in R.

 

Table 1 shows the clear structure of the distribution functions. The names of the functions always contain a d, p, q, or r in front, followed by the name of the probability distribution.

Hereby, d stands for the PDF, p stands for the CDF, q stands for the quantile functions, and r stands for the random numbers generation.

For instance, the normal distribution its PDF is obtained by dnorm, the CDF is obtained by pnorm , the quantile function is obtained by qnorm, and random number are obtained by rnorm.

Below, you can find tutorials on all the different probability distributions. Each tutorial contains reproducible R codes and many examples.

 

All Tutorials on Probability Distributions in R

 

Bernoulli Distribution in R (4 Examples) | dbern, pbern, qbern & rbern Functions

Bernoulli Distribution in R (4 Examples) | dbern, pbern, qbern & rbern Functions

Beta Distribution in R (4 Examples) | dbeta, pbeta, qbeta & rbeta Functions

Beta Distribution in R (4 Examples) | dbeta, pbeta, qbeta & rbeta Functions

Binomial Distribution in R (4 Examples) | dbinom, pbinom, qbinom & rbinom Functions

Binomial Distribution in R (4 Examples) | dbinom, pbinom, qbinom & rbinom Functions

Calculate Critical t-Value in R (3 Examples)

Calculate Critical t-Value in R (3 Examples)

Calculate Skewness & Kurtosis in R (2 Examples)

Calculate Skewness & Kurtosis in R (2 Examples)

Cauchy Density in R (4 Examples) | dcauchy, pcauchy, qcauchy & rcauchy Functions

Cauchy Density in R (4 Examples) | dcauchy, pcauchy, qcauchy & rcauchy Functions

Chi Square Distribution in R (4 Examples) | dchisq, pchisq, qchisq & rchisq Functions

Chi Square Distribution in R (4 Examples) | dchisq, pchisq, qchisq & rchisq Functions

Continuous Uniform Distribution in R (4 Examples) | dunif, punif, qunif & runif Functions

Continuous Uniform Distribution in R (4 Examples) | dunif, punif, qunif & runif Functions

Exponential Distribution in R (4 Examples) | dexp, pexp, qexp & rexp Functions

Exponential Distribution in R (4 Examples) | dexp, pexp, qexp & rexp Functions

F Distribution in R (4 Examples) | df, pf, qf & rf Functions

F Distribution in R (4 Examples) | df, pf, qf & rf Functions

Gamma Distribution in R (4 Examples) | dgamma, pgamma, qgamma & rgamma Functions

Gamma Distribution in R (4 Examples) | dgamma, pgamma, qgamma & rgamma Functions

Generate Matrix with i.i.d. Normal Random Variables in R (2 Examples)

Generate Matrix with i.i.d. Normal Random Variables in R (2 Examples)

Generate Multivariate Random Data in R (2 Examples)

Generate Multivariate Random Data in R (2 Examples)

Generate Random Values with Fixed Mean & Standard Deviation in R (2 Examples)

Generate Random Values with Fixed Mean & Standard Deviation in R (2 Examples)

Generate Set of Random Integers from Interval in R (2 Examples)

Generate Set of Random Integers from Interval in R (2 Examples)

Geometric Distribution in R (4 Examples) | dgeom, pgeom, qgeom & rgeom Functions

Geometric Distribution in R (4 Examples) | dgeom, pgeom, qgeom & rgeom Functions

Half Normal Distribution in R (4 Examples)

Half Normal Distribution in R (4 Examples)

Hypergeometric Distribution in R (4 Examples) | dhyper, phyper, qhyper & rhyper Functions

Hypergeometric Distribution in R (4 Examples) | dhyper, phyper, qhyper & rhyper Functions

Load More

 

Subscribe to the Statistics Globe Newsletter

Get regular updates on the latest tutorials, offers & news at Statistics Globe.
I hate spam & you may opt out anytime: Privacy Policy.


32 Comments. Leave new

  • Gowtham S
    December 5, 2021 10:17 am

    Hi, I am interested in learning how to R is being used in probability model. In most of the case I could see rolling a fair dice but incase of un-fair dice, how can it be approached. Please share me some resources for probability models using R.

    Reply
  • Mohammad Yarahmadi
    August 14, 2022 5:42 pm

    Hello, dear Mr. Joachim Schork
    I’m working on an article, I’m almost finished, now I need a series of x and y data, I want to see if they follow the generalized Rayleigh distribution (Burr type x) or not…
    No matter what I do, I cannot find and run the codes in R
    Thank you for your advice.

    I want to do something like this

    install.packages(“fitdistrplus”)
    library(“fitdistrplus”)
    install.packages(“VGAM”)
    library(“VGAM”)
    install.packages(“rmutil”)
    library(“rmutil”)
    ######################
    ##########################
    x=c(26,63,19,66,40,49,8,69,39,82,72,66,25,41,16,18,22,42,36,34,53,54,51,76,64,26,16,44,25,55,49,24,44,42,27,28,2)
    y=c(20,18,19,85,40,49,8,71,39,48,72,62,9,3,75,18,14,42,52,34,39,7,28,64,15,48,16,13,14,11,49,24,30,2,47,28,2)
    data=c(x=x,y=y)
    #################################
    ##########################################################
    hist(data)
    #######################
    plot(density(data))
    descdist(data, boot=10000)
    #################################
    fnorm = fitdist(data, “norm”)
    fgamma = fitdist(data, “gamma”)
    flognorm = fitdist(data, “lnorm”)
    fexp = fitdist(data, “exp”)
    ########################################
    plot.legend = c(“Normal”, “Gamma”, “LogNormal”, “Exponential”)
    dist.list = list(fnorm, fgamma, flognorm, fexp)
    denscomp(dist.list,legendtext = plot.legend)
    cdfcomp(dist.list, legendtext = plot.legend)
    ###########################################
    gofstat(dist.list , fitnames=plot.legend)
    ks.test(data, pexp, fexp$estimate[1], fexp$estimate[2])
    ks.test(data, pnorm, fnorm$estimate[1], fnorm$estimate[2])
    ks.test(data, plognorm, flognorm$estimate[1], flognorm$estimate[2])
    ks.test(data, pgamma, fgamma$estimate[1], fgamma$estimate[2])

    Reply
    • Joachim
      August 15, 2022 8:08 am

      Hey Mohammad,

      I’m not an expert on the generalized Rayleigh distribution. However, I have just tried to run your code, and it seems to work fine. Could you specify your problem in some more detail?

      Regards,
      Joachim

      Reply
  • David Bartley
    May 5, 2023 7:19 am

    Within Mathematica, CDF and quantile are easily computed, given a user-defined PDF (in addition to the common distributions). Are there similar established routines in R, or must I use R’s integrate for CDF and an inversion routine for quantile?

    Reply
    • Cansu (Statistics Globe)
      May 5, 2023 3:44 pm

      Hello David,

      It looks like you can use the integrate() function to find the cdf of the user-defined pdf. Then use the uniroot() function to find the quantiles. See the example code below.

      custom_pdf <- function(x) {
  return(3 * x^2) # Example: x^3 distribution from 0 to 1
}
 
# Compute the CDF
custom_cdf <- function(x) {
  result <- integrate(custom_pdf, lower = 0, upper = x)
  return(result$value)
}
 
# Compute the quantile
custom_quantile <- function(p) {
  result <- uniroot(function(x) custom_cdf(x) - p, interval = c(0, 1))
  return(result$root)
}
 
# Test the functions
cdf_value <- custom_cdf(0.5)
quantile_value <- custom_quantile(0.5)

      This code defines a custom PDF for x^3 distribution, computes the CDF at x = 0.5, and finds the quantile at p = 0.5.

      Reply
  • David Bartley
    May 7, 2023 2:23 pm

    Thanks so much Cansu,

    However, with:

    pdf = -1 && x<=+1) return((1/4)*(1-x)^3) else return(0) }

    When I compute pdf(-2.10), pdf(-2), pdf(-1.5), pdf(.5), etc. pdf is computed correctly.

    But your program:

    cdf <- function(x) { result = -1 && x <= +1 : 'length = 101' in coercion to 'logical(1)'

    Thanks,

    David

    Reply
  • David Bartley
    May 8, 2023 9:55 am

    Cansu,

    I don’t know how my message to you became so entirely corrupted. Let me start over. First of all, the probability distribution function pdf is defined as:

    pdf = -1 && x= -1 && x 0.

    cdf may be defined as:

    cdf <- function(x) {
    result 0.

    My questions:

    (1) Why the original error message?

    (2) Is there a simple way to plot from x = −1 to x = 1?

    Thanks,

    David

    Reply
  • David Bartley
    May 8, 2023 9:59 am

    Cansu,

    Again, my message is corrupted. There is something wrong with this method of messaging. Can I email you my question somehow?

    David

    Reply
  • David Bartley
    May 8, 2023 11:00 am

    Cansu,

    This message system is not working. Could you send me an email address so as to send you my questions?

    Thanks,

    David

    Reply
    • Cansu (Statistics Globe)
      May 8, 2023 11:14 am

      Hello David,

      I am so sorry, I don’t share my private email. It is strange that the messaging system doesn’t work for you. Because I have been answering comments for months in the comment sections, and no one has mentioned about that. If you mean that you can not see your message after posting it, then it is totally normal. Because the messages are posted after our approval to avoid scams.

      Regards,
      Cansu

      Reply
  • David Bartley
    May 8, 2023 11:34 am

    Cansu,

    Maybe my browser is not working correctly, so let me switch to another.

    First of all, the probability distribution function pdf is defined as:

    pdf = -1 && x= -1 && x 0.

    cdf may be similarly fixed with “Vectorize” as:

    cdf <- function(x) {
    result 0.

    My questions:

    (1) Why the original error message?
    (2) Is there a simple way to plot from x = −1 to x = 1?

    Thanks,

    David

    Reply
  • David Bartley
    May 8, 2023 11:36 am

    No. For some reason, the definition for pdf, etc. becomes gibberish. I’m giving up for now.

    David

    Reply
  • David Bartley
    May 9, 2023 8:03 am

    Cansu,

    Try reading my questions saved at Dropbox:

    https://www.dropbox.com/s/eziacwi7jzi3j8f/To%20Cansu.rtf?dl=0https://www.dropbox.com/s/eziacwi7jzi3j8f/To%20Cansu.rtf?dl=0

    Thanks,

    David

    Reply
    • Cansu (Statistics Globe)
      May 9, 2023 9:36 am

      Hello David,

      The problem is you don’t let the function take multiple values; that is the first problem. As you figured out, you need a vector as an input. Also, you should modify the if statement a bit since the loop will be terminated when you use return(). You should initialize a results vector, append each result one by one, and return it. See below.

      pdf <- function(x) {                   # define function 
  result <- numeric(length(x))
 
  for (i in 1:length(x)) {
    if (x[i] >= -1 && x[i] <= 1) {
      result[i] <- (1 / 4) * (1 - x[i])^3
    } else {
      result[i] <- 0
    }
  }
 
  return(result)
}
 
y <- seq(-1,1,0.01)                     # define input 
values<-pdf(y)                          # define output 
values[1:5]                             # print first 5 values 
# [1] 2.000000 1.970150 1.940598 1.911343 1.882384
 
plot(values) # plot function

      But there is a simple way to plot a function using the stat_function layer of ggplot2. See below.

      library(ggplot2)                        # do all using ggplot2 library 
ggplot(data.frame(values = c(-1, 1)), aes(values)) +
  stat_function(fun = pdf, color = "blue", size = 1)

      I hope these solutions help.

      Regards,
      Cansu

      Reply
  • David Bartley
    May 10, 2023 1:27 am

    Cansu,

    Thanks for answering.

    No, there is no loop. Any looping would be done within the plot routine and should be entirely invisible to the user. Also, the error message after plot() was really peculiar, giving no clue as to its resolution. In fact, resolution could possibly be done within the plot() routine itself. This must be a recurring problem within R.

    I do not have ggplot2. Does plot(), have options for specifying the frame range (e.g., −1 to +1 in my sample case)? The plotting does work correctly for x = 0 to 1 as long as “Vectorize” is used.

    This is all really cumbersome and could make addressing more serious applications next to impossible. I’m guessing that R is simply not set up to do such calculations and is mainly for analyzing a variety of datasets.

    David

    Reply
    • Cansu (Statistics Globe)
      May 10, 2023 7:31 am

      Hello David,

      Sorry, I shared the wrong code for the first solution. Please see the following for plotting via plot().

      pdf <- function(x) {                   # define function 
  result <- numeric(length(x))
 
  for (i in 1:length(x)) {
    if (x[i] >= -1 && x[i] <= 1) {
      result[i] <- (1 / 4) * (1 - x[i])^3
    } else {
      result[i] <- 0
    }
  }
 
  return(result)
}
 
y <- seq(-1,1,0.01)                     # define input 
values<-pdf(y)                          # define output 
values[1:5]                             # print first 5 values 
# [1] 2.000000 1.970150 1.940598 1.911343 1.882384
 
plot(values) # plot function

      Also, you can install the ggplot2 package easily as follows.

      install.packages("ggplot2")
library(ggplot2)                        # do all using ggplot2 library 
ggplot(data.frame(values = c(-1, 1)), aes(values)) +
  stat_function(fun = pdf, color = "blue", size = 1)

      I think it is easier to plot such functions using ggplot2. Sorry for the inconvenience again.

      Regards,
      Cansu

      Reply
  • David Bartley
    May 12, 2023 8:29 am

    Cansu,

    OK. Here’s my question:

    Suppose you define an array y as you did:

    y <- seq(-1,1,0.01)

    Then a common function like sin() in R with argument y returns an array:

    sin(y)

    Now then, suppose I define a function pdf via the simple expression:

    pdf = -1 && x= -1 && x <= +1 : 'length = 201' in coercion to 'logical(1)'

    Why? Why must we resort to your complicated definition of pdf?

    David

    Reply
  • David Bartley
    May 12, 2023 8:37 am

    Again, on replying to you, 4 lines of my reply were strangely deleted. The end should read:

    Now then, suppose I define a function pdf via the simple expression:

    pdf = -1 && x= -1 && x <= +1 : 'length = 201' in coercion to 'logical(1)'

    Why? Why must we resort to your complicated definition of pdf?

    David

    Reply
  • David Bartley
    May 12, 2023 8:39 am

    Again, lines deleted.

    Reply
  • David Bartley
    May 12, 2023 8:41 am

    Maybe there’s an invisible character in my text that throws the comment box off.

    Reply
  • David Bartley
    May 12, 2023 8:52 am

    Anyway, my earlier simple definition of pdf, just like sin, computes a value for any individual argument x (e.g., -.2,0,.4, etc.).

    However, unlike sin, my pdf with argument y, pdf(y), does not return an array, but gives the peculiar error:

    Error in x >= -1 && x <= +1 : 'length = 201' in coercion to 'logical(1)'

    Why? Why must we resort to your complicated definition of pdf?

    David

    Reply
  • David Bartley
    May 12, 2023 9:19 am

    Cansu,

    I finally figured out how to use “plot”. With my simpler scalar definition of pdf, as I mentioned earlier, plot(Vectorize(pdf) correctly plots for x > 0. At last, I found that plot(Vectorize(pdf, −2, 2) also correctly plots for −2 < x = -1 && x <= +1 : 'length = 201' in coercion to 'logical(1)'

    and found out that this sort of problem began with version 4.2.1

    David

    Reply
  • David Bartley
    May 12, 2023 9:27 am

    Typos: Should be plot(Vectorize(pdf)) and plot(Vectorize(pdf), −2, 2)

    Reply
  • David Bartley
    May 12, 2023 5:12 pm

    Cansu,

    Now here is something interesting. Using abs(x)= -1 && x<=+1) as condition does not require Vectorize for plot or other functions.

    For example, try:

    pdf<-function(x) { ifelse(abs(x)= -1 && x <= +1 : 'length = 101' in coercion to 'logical(1)'

    does not appear.

    David

    Reply
  • David Bartley
    May 12, 2023 5:25 pm

    Again, the Comment box deleted lines. Here is what I was just now trying to send you:

    https://www.dropbox.com/s/ybe31awu7bsnj49/To%20Cansu%202.rtf?dl=0

    David

    Reply
    • Cansu (Statistics Globe)
      May 15, 2023 6:51 am

      Hello David,

      I understand that you managed to use the function the way you liked it in the end. I am happy to hear that. If you have any questions regarding the provided solution by me, let me know.

      Regards,
      Cansu

      Reply
  • David Bartley
    May 18, 2023 7:43 am

    Cansu,

    Please see thank you note:

    https://www.dropbox.com/s/7ufpxmur9aabp2e/To%20Cansu%203.rtf?dl=0

    You might be located in the UK somewhere, since you’re at work while I’m night-owling!

    David

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

Fill out this field
Fill out this field
Please enter a valid email address.

Top