Random Numbers in R (2 Examples) | Draw Randomly from Probability Distribution & Given Data

In this article, I’ll explain how to draw random numbers in R programming.

Table of contents:

• Example 1: Draw Random Numbers from Probability Distribution
• Example 2: Draw Random Numbers from Given Data
• Video & Further Resources

So without further ado, here’s the step-by-step process.

Example 1: Draw Random Numbers from Probability Distribution

Example 1 explains how to simulate a set of random numbers according to a probability distribution in R. I’ll illustrate this procedure based on the normal distribution.

Before we can generate a set of random numbers in R, we have to specify a seed for reproducibility and a sample size of random numbers that we want to draw:

set.seed(13579)                        # Set seed
N <- 10000                             # Sample size

We then can use the rnorm R function to produce N normally distributed random numbers:

rand1 <- rnorm(N)                      # Normally distributed random values
rand1                                  # Print random numbers to RStudio console
# -1.234715493 -1.252833873 -0.254778031 -1.526646627...

The RStudio console shows the output of the rnorm function: 1000 random numbers. We can illustrate the distribution of these random numbers in a histogram with the hist function:

hist(rand1, breaks = 100)              # Histogram of random numbers

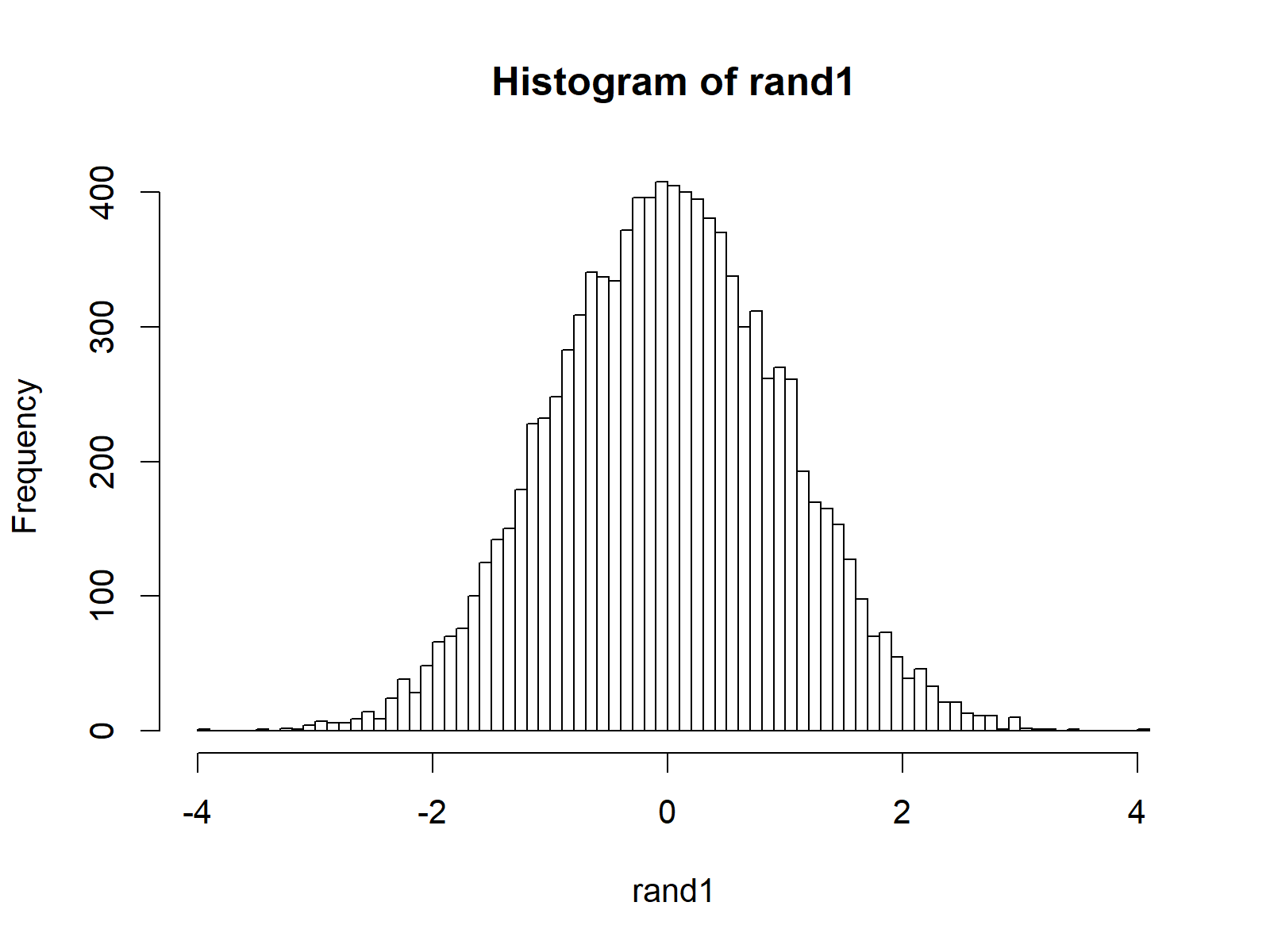
Figure 1: Histogram Illustrating the Distribution of Randomly Drawn Values.

Figure 1 shows the output of the previous R code. As you can see, our random values are almost perfectly normally distributed.

The small peaks in the distribution are due to random noise. The larger the sample size gets, the smoother the normal distribution of our random values will be.

Note: In this example, I’ve shown you how to draw random numbers from a normal distribution. However, the R programming language provides functions to simulate random data according to many different probability distributions (e.g. uniform distribution, binomial distribution, logistic distribution, exponential distribution, and so on…). You can learn more about the different R commands for the generation of random numbers from different distributions in this tutorial.

Example 2: Draw Random Numbers from Given Data

In the second example, I’ll show you how to draw random numbers from some given data. First, let’s create some example data:

x <- 1:100                             # Create example data
x                                      # Print example data to RStudio console
#  1   2   3   4   5   6   7   8   9  10  11  12  13...

As you can see based on the RStudio console output, our example data is a simple numeric vector with a range of integers from 1 to 100.

We can now use the sample function of the R programming language to draw a random subset of our example data. In this example, I’ll draw a sample size of 10 cases:

sample(x, 10)                          # Simple random sampling from example data
# 99  16  68 100  73  60   9  67  10  81

The output of the sample function is shown above. A vector with 10 numbers within the range from 1 to 100.

Video & Further Resources

If you need more info on the examples of this tutorial, I can recommend to have a look at the following video of the Statistics Globe YouTube channel. In the video, I show the content of this tutorial.

The YouTube video will be added soon.

You might also have a look at the other tutorials on distributions and the generation of random numbers in R programming:

• Bernoulli Distribution in R
• Beta Distribution in R
• Binomial Distribution in R
• Bivariate & Multivariate Distributions in R
• Cauchy Distribution in R
• Chi-Squred Distribution in R
• Exponential Distribution in R
• F Distribution in R
• Gamma Distribution in R
• Geometric Distribution in R
• Hypergeometric Distribution in R
• Log Normal Distribution in R
• Logistic Distribution in R
• Negative Binomial Distribution in R
• Normal Distribution in R
• Poisson Distribution in R
• Student t Distribution in R
• Studentized Range Distribution in R
• Uniform Distribution in R
• Weibull Distribution in R
• Wilcoxon Signedank Statistic Distribution in R
• Wilcoxonank Sum Statistic Distribution in R

Furthermore, you may want to have a look at the related tutorials of this website.

• R Graphics Gallery
• R Functions List (+ Examples)
• The R Programming Language

In this R programming post you learned how to generate a sequence of random numbers. If you have any additional questions, don’t hesitate to let me know in the comments section.