Exponential Distribution in R (4 Examples) | dexp, pexp, qexp & rexp Functions

This tutorial explains how to apply the exponential functions in the R programming language.

The content of the article looks as follows:

• Example 1: Exponential Density in R (dexp Function)
• Example 2: Exponential Cumulative Distribution Function (pexp Function)
• Example 3: Exponential Quantile Function (qexp Function)
• Example 4: Random Number Generation (rexp Function)
• Video & Further Resources

Let’s get started…

Example 1: Exponential Density in R (dexp Function)

Let’s begin with the exponential density.

We can use the dexp R function return the corresponding values of the exponential density for an input vector of quantiles.

Let’s create such a vector of quantiles in RStudio:

x_dexp <- seq(0, 1, by = 0.02)                     # Specify x-values for exp function

Now, we can apply the dexp function with a rate of 5 as follows:

y_dexp <- dexp(x_dexp, rate = 5)                   # Apply exp function

We can use the plot function to create a graphic, which is showing the exponential density based on the previously specified input vector of quantiles:

plot(y_dexp)                                       # Plot dexp values

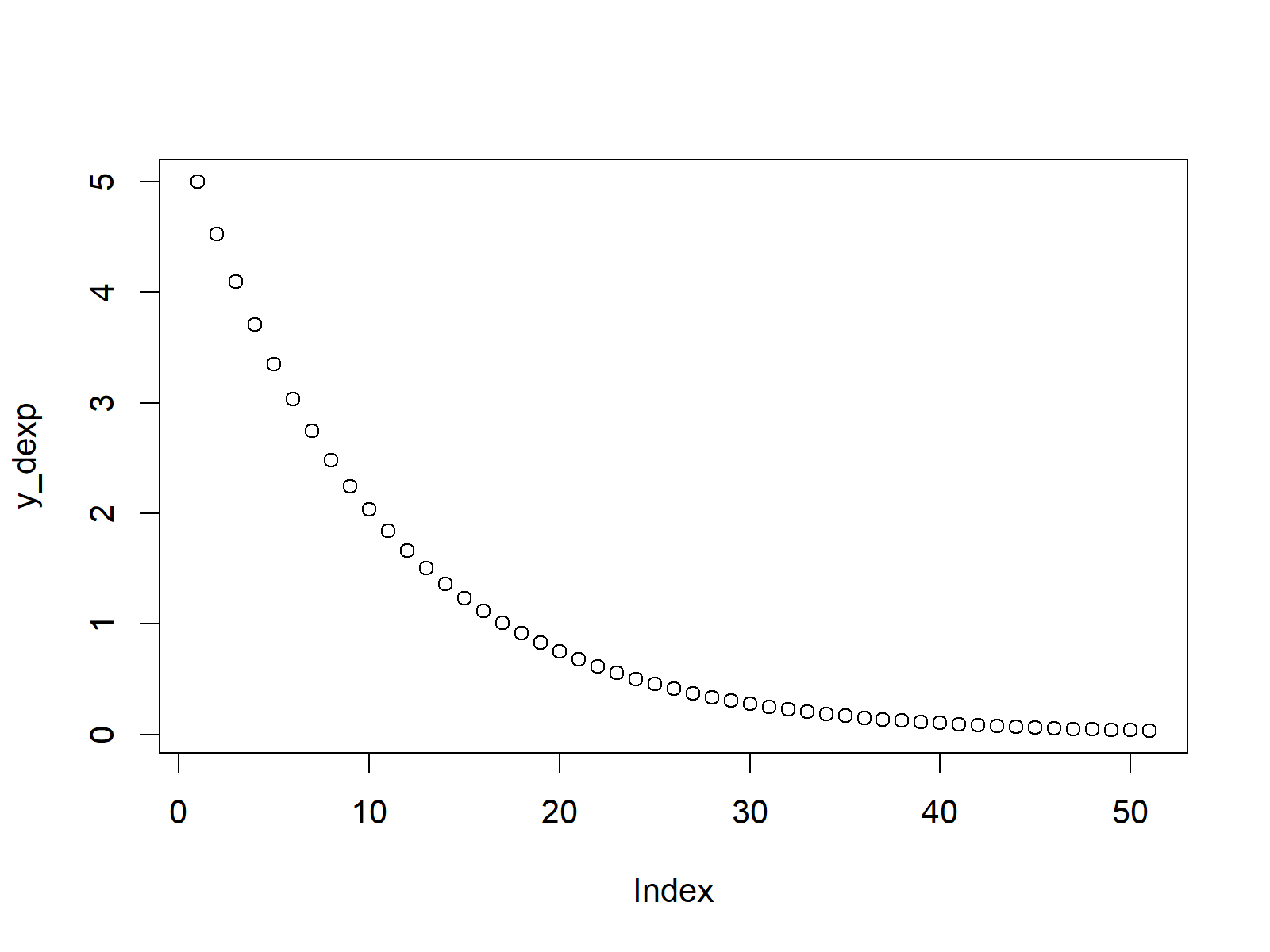
Figure 1: Exponential Density in R.

Example 2: Exponential Cumulative Distribution Function (pexp Function)

We can also use the R programming language to return the corresponding values of the exponential cumulative distribution function for an input vector of quantiles. Again, let’s create such an input vector:

x_pexp <- seq(0, 1, by = 0.02)                     # Specify x-values for pexp function

In order to get the values of the exponential cumulative distribution function, we need to use the pexp function:

y_pexp <- pexp(x_pexp, rate = 5)                   # Apply pexp function

We can draw a plot of our previously extracted values as follows:

plot(y_pexp)                                       # Plot pexp values

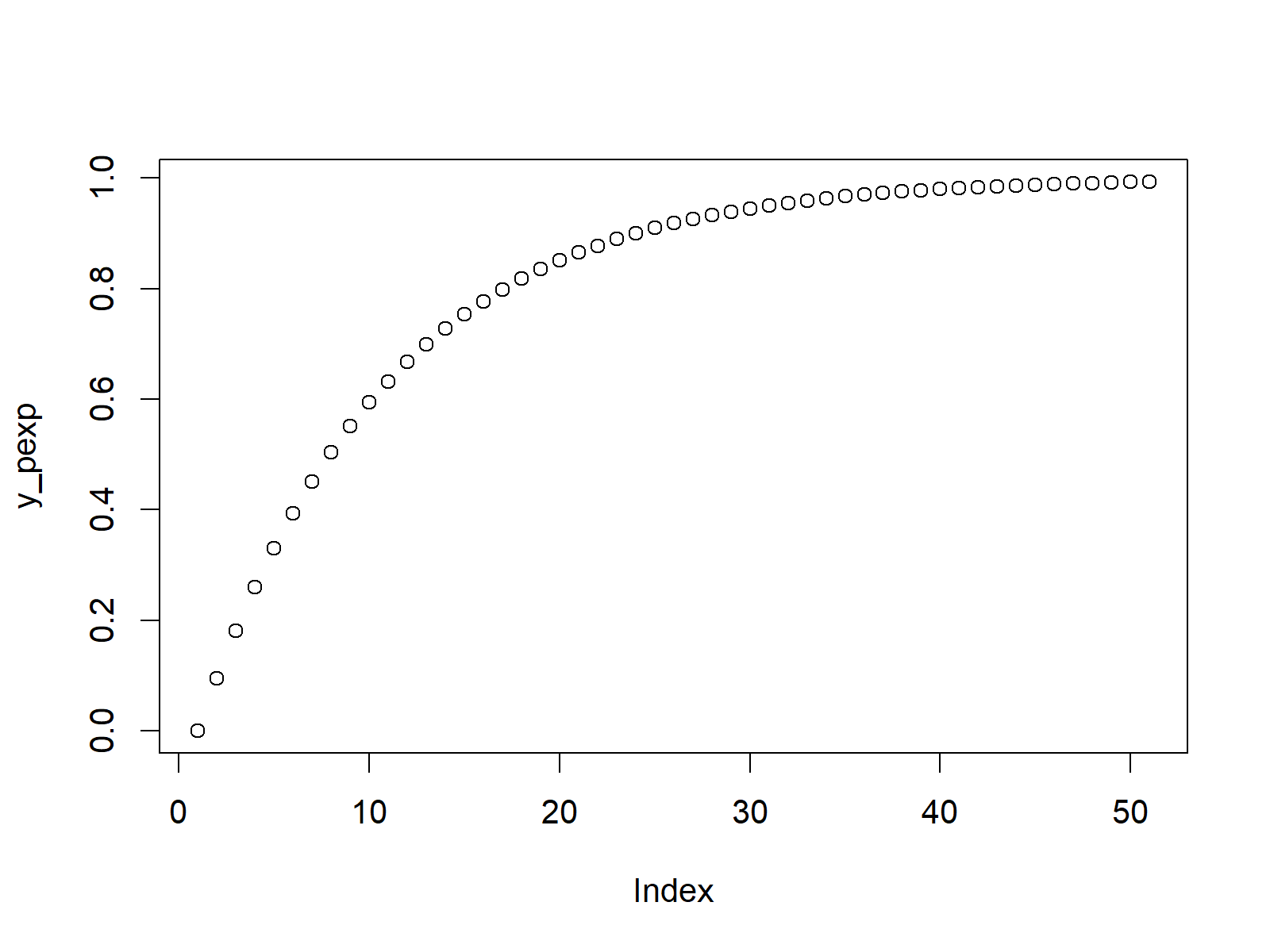
Figure 2: Exponential Cumulative Distribution Function.

Example 3: Exponential Quantile Function (qexp Function)

Similar to Examples 1 and 2, we can use the qexp function to return the corresponding values of the quantile function. This time, we need to specify a vector oft probabilities:

x_qexp <- seq(0, 1, by = 0.02)                     # Specify x-values for qexp function

The qexp command can then be used to get the quantile function values…

y_qexp <- qexp(x_qexp, rate = 5)                   # Apply qexp function

…and we can also draw a scatterplot containing these values:

plot(y_qexp)                                       # Plot qexp values

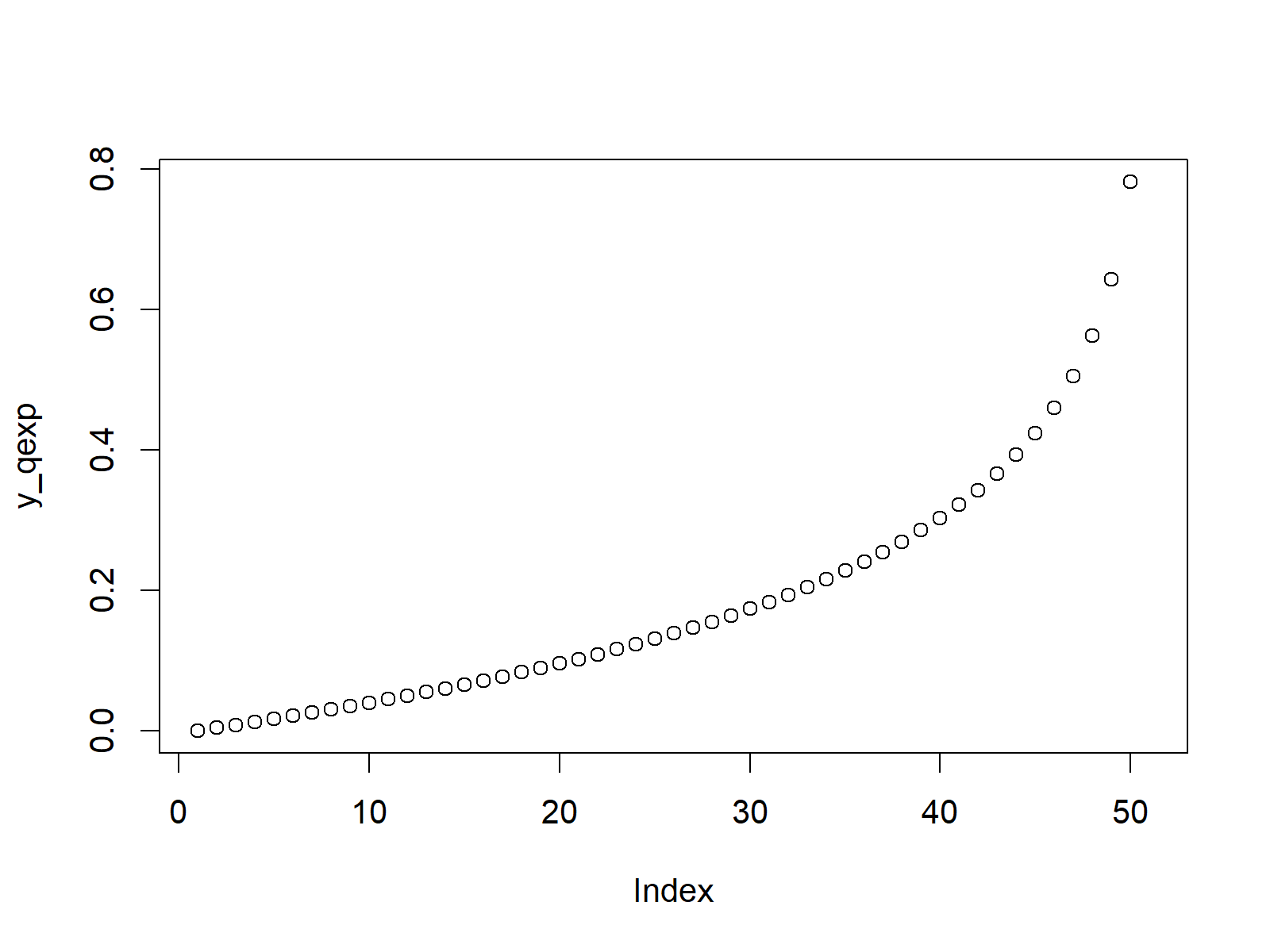
Figure 3: Exponential Quantile Function.

Example 4: Random Number Generation (rexp Function)

In R, we can also draw random values from the exponential distribution.

First, we need to specify a seed and the sample size we want to simulate:

set.seed(13579)                                    # Set seed for reproducibility
N <- 10000                                         # Specify sample size

Then, we can use the rexp function as follows:

y_rexp <- rexp(N, rate = 5)                        # Draw N exp distributed values
y_rexp                                             # Print values to RStudio console

We can create a histogram of our randomly sampled values as follows:

hist(y_rexp, breaks = 100, main = "")              # Plot of randomly drawn exp density

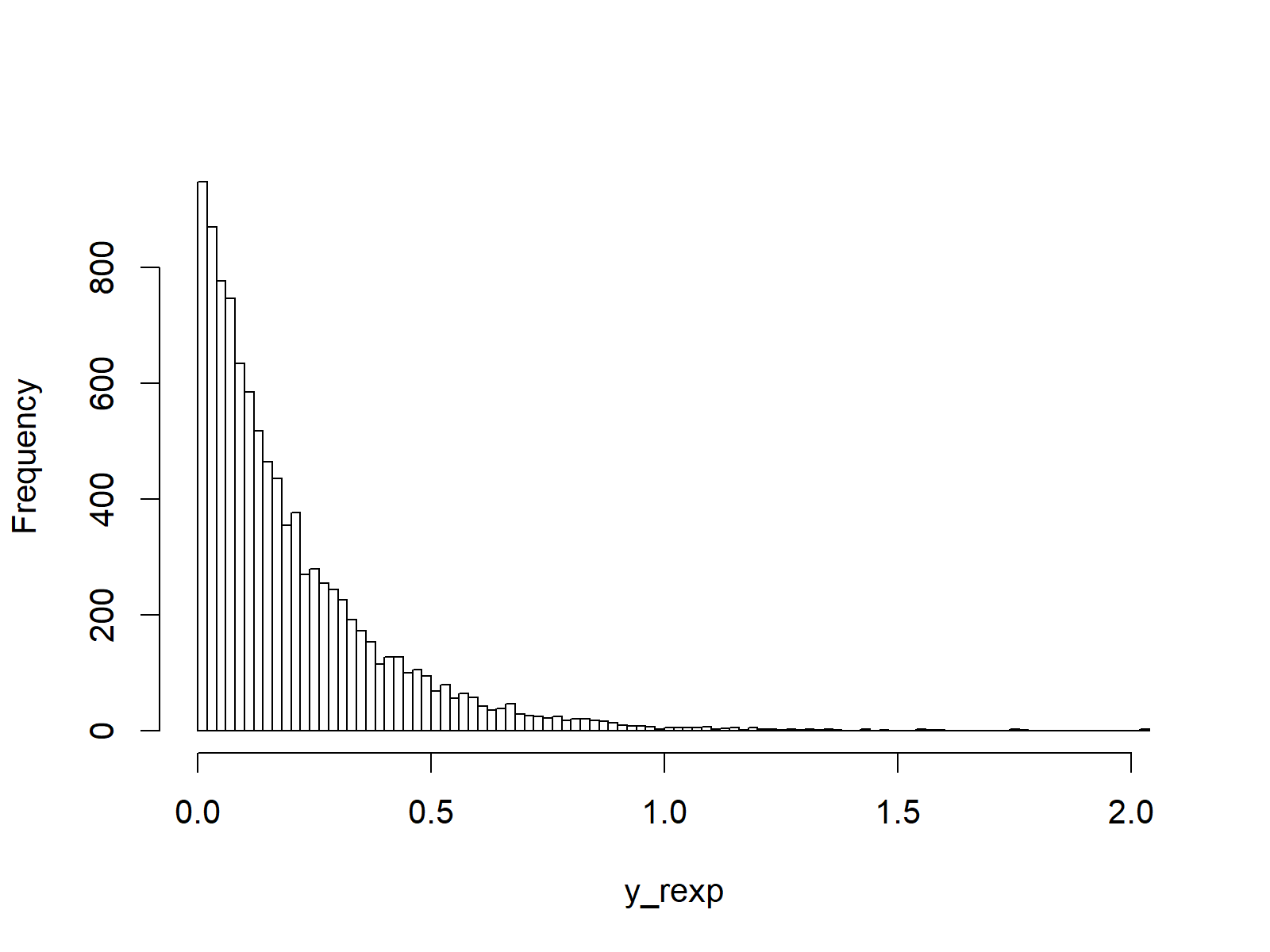
Figure 4: Histogram of Random Numbers Drawn from Exponential Distribution.

Video & Further Resources

If you need further info on the examples of this article, you may want to have a look at the following video of the Statistics Globe YouTube channel. I’m explaining the R programming code of this tutorial in the video.

The YouTube video will be added soon.

You might also read the other tutorials on probability distributions and the generation of random numbers in R:

• Bernoulli Distribution in R
• Beta Distribution in R
• Binomial Distribution in R
• Bivariate & Multivariate Distributions in R
• Cauchy Distribution in R
• Chi-Squred Distribution in R
• Exponential Distribution in R
• F Distribution in R
• Gamma Distribution in R
• Geometric Distribution in R
• Hypergeometric Distribution in R
• Log Normal Distribution in R
• Logistic Distribution in R
• Negative Binomial Distribution in R
• Normal Distribution in R
• Poisson Distribution in R
• Student t Distribution in R
• Studentized Range Distribution in R
• Uniform Distribution in R
• Weibull Distribution in R
• Wilcoxon Signedank Statistic Distribution in R
• Wilcoxonank Sum Statistic Distribution in R

In addition, you may read some of the other articles of my homepage:

• R Graphics Gallery
• R Functions List (+ Examples)
• The R Programming Language

In this post, I explained how to use the exponential functions and how to simulate random numbers with exponential growth in R. In case you have any further comments or questions, please let me know in the comments.