Datasets for PCA (Free CSV Download)

In this article, I’ll provide some example datasets for the application of a Principal Component Analysis (PCA).

Furthermore, I explain how to apply a PCA to one of those datasets in R programming. The data is provided as CSV files, though, so you may also use it to apply a PCA in other programming languages such as Python, MATLAB, SAS, and so on.

Table of contents:

With that, let’s dive into it…

Example 1: Synthetic Dataset with 200 Observations & 16 Variables

The first dataset can be downloaded as a CSV file by clicking here.

The data contains 200 rows, 15 predictor variables called x1-x15 as well as a target variable called y.

The first six rows of this dataset are illustrated in the table below:

#      x1    x2    x3   x4    x5   x6    x7    x8    x9   x10   x11   x12   x13    x14   x15     y
# 1 -4.44  0.99  2.92 3.24 10.02 2.65 -2.10 -1.76 -3.24  6.95 -1.08 -2.11 -4.92 -13.50 -3.09 -0.47
# 2 13.92  1.51  2.93 3.81 -3.15 2.20 -5.39  1.84 -2.70 -0.39  0.02  5.01 -2.22  -0.55 -0.98  0.99
# 3  4.57  0.48 -0.62 4.52  1.41 1.35  4.95  1.51  4.12 -1.10  0.46 -0.85  2.38  -5.09  0.70  1.36
# 4  6.58  1.48 -0.90 1.74  0.79 1.98  4.10  0.93  0.71 -2.11 -1.80  5.43  2.15  -0.24  0.57  1.43
# 5  1.78  2.84  3.61 0.05 -0.33 2.49  0.72  1.28  2.06  3.86  0.57  3.33 -1.26   0.64 -6.14  1.03
# 6  4.73 -0.30 -1.23 4.98 -0.09 1.24 -4.92  3.71 -0.58 -0.94 -2.51  8.97  0.97  -0.30  1.61  1.02

The correlation matrix of these variables looks as follows:

#        x1    x2    x3    x4    x5    x6    x7    x8    x9   x10   x11   x12   x13   x14   x15     y
# x1   1.00 -0.01  0.03 -0.04 -0.43 -0.04  0.06  0.01  0.09 -0.10 -0.05  0.03 -0.33  0.38  0.08  0.47
# x2  -0.01  1.00  0.01 -0.03  0.14  0.05  0.04 -0.55 -0.04  0.33  0.00 -0.03 -0.12  0.01 -0.59  0.03
# x3   0.03  0.01  1.00 -0.03 -0.06 -0.49 -0.09 -0.37 -0.06  0.03  0.01  0.04 -0.02  0.01 -0.45 -0.05
# x4  -0.04 -0.03 -0.03  1.00  0.00  0.02 -0.54  0.01 -0.11  0.03 -0.32 -0.18  0.09 -0.02  0.02  0.07
# x5  -0.43  0.14 -0.06  0.00  1.00 -0.03 -0.07  0.02 -0.10  0.09  0.00 -0.32 -0.31 -0.49 -0.16 -0.33
# x6  -0.04  0.05 -0.49  0.02 -0.03  1.00  0.06 -0.03  0.05  0.17  0.03  0.02  0.02  0.06  0.29  0.24
# x7   0.06  0.04 -0.09 -0.54 -0.07  0.06  1.00  0.00  0.46 -0.03  0.05  0.11 -0.01  0.08  0.03  0.30
# x8   0.01 -0.55 -0.37  0.01  0.02 -0.03  0.00  1.00  0.10 -0.36 -0.01 -0.06  0.00 -0.04  0.32 -0.03
# x9   0.09 -0.04 -0.06 -0.11 -0.10  0.05  0.46  0.10  1.00 -0.02  0.06  0.07 -0.03  0.11  0.07  0.40
# x10 -0.10  0.33  0.03  0.03  0.09  0.17 -0.03 -0.36 -0.02  1.00 -0.03 -0.02  0.01 -0.05 -0.61  0.14
# x11 -0.05  0.00  0.01 -0.32  0.00  0.03  0.05 -0.01  0.06 -0.03  1.00  0.15  0.00 -0.02  0.02  0.03
# x12  0.03 -0.03  0.04 -0.18 -0.32  0.02  0.11 -0.06  0.07 -0.02  0.15  1.00  0.02  0.22  0.05  0.32
# x13 -0.33 -0.12 -0.02  0.09 -0.31  0.02 -0.01  0.00 -0.03  0.01  0.00  0.02  1.00  0.26  0.09  0.20
# x14  0.38  0.01  0.01 -0.02 -0.49  0.06  0.08 -0.04  0.11 -0.05 -0.02  0.22  0.26  1.00  0.08  0.75
# x15  0.08 -0.59 -0.45  0.02 -0.16  0.29  0.03  0.32  0.07 -0.61  0.02  0.05  0.09  0.08  1.00  0.04
# y    0.47  0.03 -0.05  0.07 -0.33  0.24  0.30 -0.03  0.40  0.14  0.03  0.32  0.20  0.75  0.04  1.00

As you can see, some of the variables are correlated, so there might be a good chance to reduce the dimensionality of these data by applying a PCA.

Later, I’ll demonstrate how to do this. However, first I want to provide some alternative datasets for the application of a PCA.

Example 2: Synthetic Dataset with 1000 Observations & 51 Variables

This dataset can be downloaded here.

It contains 1000 rows, 50 predictor columns x1-x50, as well as a target variable called y.

Again, some of the variables are correlated, but others are uncorrelated.

Example 3: Synthetic Dataset with 10000 Observations & 201 Variables

The third synthetic dataset can be downloaded here.

This is the largest dataset and contains 10000 rows, 200 predictor variables called x1-x200, and a target variable called y.

As in the previous datasets, there are some correlations in the data.

Application of PCA to Example Dataset

This section demonstrates how to apply a Principal Component Analysis to our first example dataset. I’ll use the R programming language for this task.

As a first step, we have to download the CSV (see Example 1 above) and import the data into R:

df <- read.csv2("... Insert Your File Path .../data_pca_200x16.csv")

Furthermore, we have to install and load the factoextra and ggplot2 packages:

install.packages("factoextra")
install.packages("ggplot2")
 
library("factoextra")
library("ggplot2")

Next, we can use the prcomp function to apply a PCA to our data:

pca_object <- prcomp(df[ , colnames(df) != "y"],
                     scale = TRUE)

The previous code created the data object pca_object, which contains all relevant information of our PCA.

In the next step, we have to find out the optimal number of components for our PCA. We can do that using a scree plot:

fviz_eig(pca_object,
         addlabels = TRUE,
         choice = "eigenvalue",
         ncp = 25) + 
  geom_hline(yintercept = 1,
             linetype = "dashed",
             color = "red")

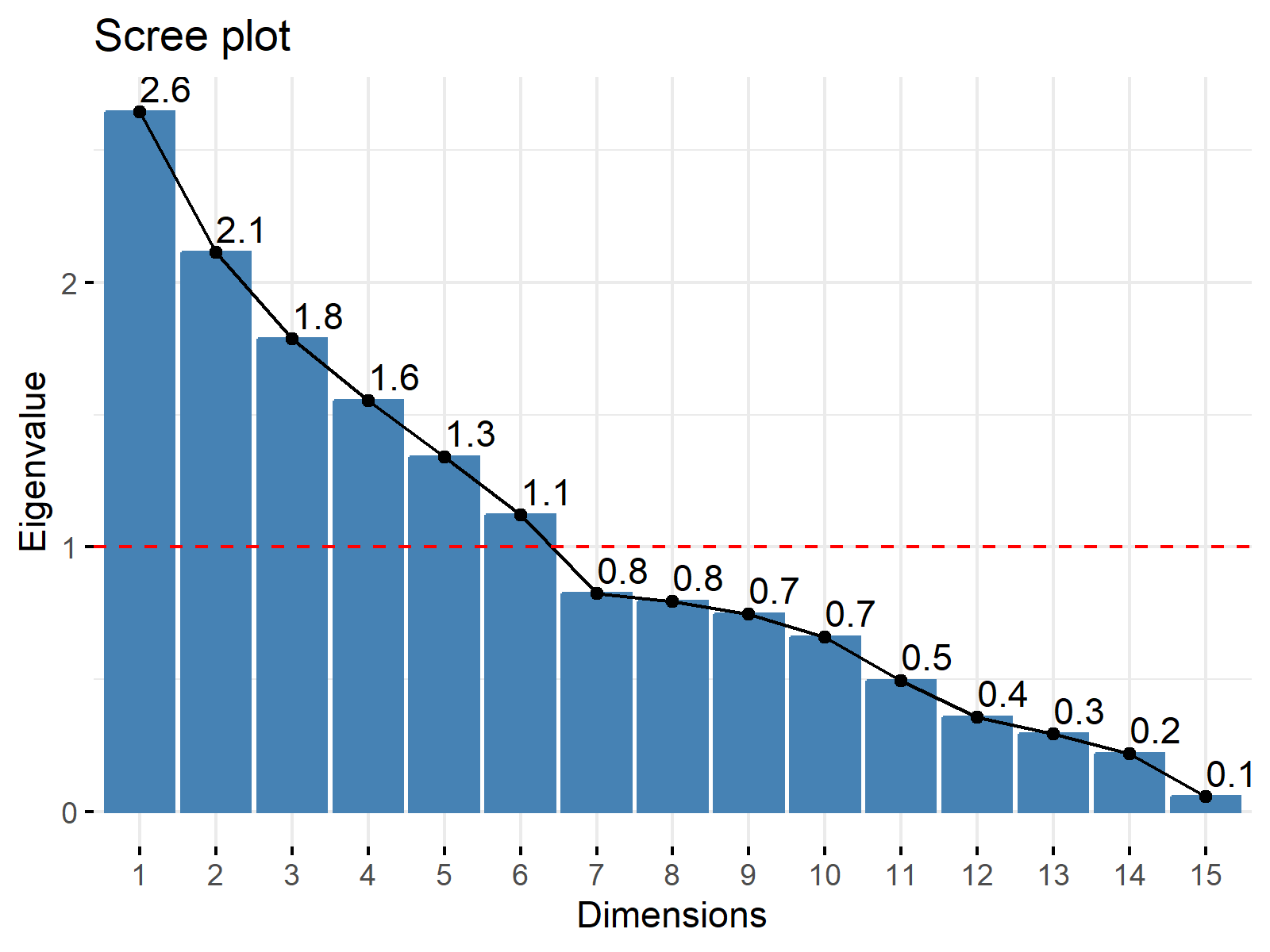
Based on the Kaiser Rule, we select six components:

pca_num <- sum(pca_object$sdev^2 > 1)
pca_num
# [1] 6

Next, we may extract those six components and store them in a new data frame:

df_pca <- as.data.frame(pca_object$x)[ , 1:pca_num]

Furthermore, we may add our target variable y to this data frame:

df_pca$y <- df$y
head(df_pca)
#          PC1        PC2        PC3        PC4         PC5        PC6     y
# 1 -4.5673859  3.8391534  0.5400235 -0.6327482  0.02467123  0.6370757 -0.47
# 2 -0.6986954  0.1487121 -2.7598959 -0.2851226 -0.97495179  2.3833532  0.99
# 3  0.3155903  0.7012377  0.7704211 -0.4115533  0.31695790 -1.7477572  1.36
# 4  0.3089375 -0.1835249 -0.3584449 -1.0258141  0.08567788 -0.6375365  1.43
# 5 -2.5756827 -1.0124390  0.1941711 -0.5682977  0.60375974 -0.1018536  1.03
# 6  0.9047002  1.4767408 -2.4195776 -0.9293660  0.23401615  0.4243889  1.02

The previous table shows our final PCA dataset. It contains the six most relevant components as well as our target variable. As you can see, we have heavily reduced the dimensions of our data (i.e. from 16 to 7 variables).

We might now do certain data analyses such as clustering, classification, or basically any machine learning method that comes to our mind.

For the sake of simplicity, I’ll just perform a liner regression based on our PCA dataset:

summary(lm(y ~ ., df_pca))
# Call:
# lm(formula = y ~ ., data = df_pca)
# 
# Residuals:
#      Min       1Q   Median       3Q      Max 
# -1.00982 -0.28340  0.00316  0.25346  1.10235 
# 
# Coefficients:
#             Estimate Std. Error t value Pr(>|t|)    
# (Intercept)  1.37535    0.02871  47.910  < 2e-16 ***
# PC1          0.09742    0.01770   5.504 1.17e-07 ***
# PC2         -0.27070    0.01980 -13.674  < 2e-16 ***
# PC3         -0.07028    0.02153  -3.264 0.001299 ** 
# PC4         -0.16624    0.02309  -7.200 1.31e-11 ***
# PC5         -0.06431    0.02485  -2.588 0.010384 *  
# PC6         -0.10560    0.02719  -3.884 0.000141 ***
# ---
# Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# Residual standard error: 0.406 on 193 degrees of freedom
# Multiple R-squared:  0.6098,	Adjusted R-squared:  0.5976 
# F-statistic: 50.26 on 6 and 193 DF,  p-value: < 2.2e-16

As demonstrated by the output above, all our components have a significant predictive power for our target variable y.

Please note that this demonstration of a PCA just meant to give a brief overview on this method. In case you are interested in further details, please take a look at our main PCA article.

Fields of PCA Application & Real Example Datasets

In the previous sections, I provided some synthetic datasets for the application of a PCA.

While this has many advantages for teaching purposes, it has the drawback that the data does not have any meaning.

However, depending on your field of study, you might be interested in a more realistic dataset.

Some popular more realistic datasets for the application of a PCA are the iris flower dataset, mtcars, and decathlon2.

Here is a list of fields, where PCA is regularly applied. You might search for the term “PCA dataset” in combination with your specific research field:

• Biology and Biomedicine:
• Genomics: Analyzing gene expression data.
• Proteomics: Determining protein expression profiles.
• Neuroimaging: Analyzing brain activity from fMRI or EEG data.
• Chemistry:
• Spectroscopy: Analyzing data from techniques like NMR, MS, or UV-Vis.
• Chemometrics: Analyzing chemical data to extract meaningful information.
• Psychology:
• Psychometrics: Analyzing personality tests, intelligence tests, etc.
• Finance and Economics:
• Portfolio Analysis: Understanding asset patterns and their contributions to risk and return.
• Geology and Environmental Science:
• Remote Sensing: Reducing dimensionality in satellite or drone imagery.
• Climatology: Analyzing large datasets of climate variables.
• Computer Science and Engineering:
• Image Processing: Reducing the dimensionality of image data.
• Machine Learning: Preprocessing datasets before applying algorithms.
• Signal Processing: Analyzing and representing signals in a compact form.
• Sociology and Anthropology:
• Survey Data Analysis: Breaking down and understanding large survey datasets.
• Linguistics:
• Semantic Analysis: Understanding patterns in large textual datasets.
• Marketing and Business:
• Customer Segmentation: Grouping similar customers based on purchasing behaviors or other metrics.
• Product Recommendation: Understanding product features that drive sales.
• Astronomy:
• Star and Galaxy Analysis: Reducing the dimensionality of datasets about star or galaxy properties.

Video, Further Resources & Summary

Do you need more explanations on how to apply a PCA? Then you might want to have a look at the following video on my YouTube channel. In the video, Cansu Kebabci and I illustrate the theoretical concepts of Principal Component Analyses:

Besides that, you might read the other tutorials on my homepage:

• Visualization of PCA in R
• Principal Component Analysis in R
• Principal Component Analysis in Python
• Statistical Methods Explained
• R Programming Examples

In summary: In this tutorial you have learned how to apply a PCA in the R programming language. Please let me know in the comments, in case you have any additional questions.