Missing Values – Statistical Analysis & Handling of Incomplete Data
Missing data (or missing values) appear when no value is available in one or more variables of an individual.
Missing data can occur due to several reasons, e.g. interviewer mistakes, anonymization purposes, or survey filters.
However, most of the time data is missing as result of a refusal to respond by the participant (also called item nonresponse).
Nonresponse has different causes such as a lack of knowledge about the question, an abortion of the questionnaire, or the unwillingness to respond to sensitive questions.
Missing values are an issue of essentially every survey – They might introduce bias in your estimates and may therefore lead to wrong conclusions of your survey.
In the following article, I’m going to show everything you need to know in order to handle missing data in an appropriate way.
Types of Missing Data (What are Response Mechanisms?)
Due to its serious effect on survey results, it is important to understand the reasons for missing values.
Incomplete data is usually categorized into three different response mechanisms: Missing Completely At Random (MCAR); Missing At Random (MAR); and Missing Not At Random (MNAR or NMAR) (Little & Rubin, 2002).
Consider X as a set of auxiliary variables, Y as our variable of interest, and P as the response propensity, i.e. the probability of an individual to respond to a question.
Missing Completely At Random (MCAR)
- P neither depends on X nor on Y.
- Example: Some responses were accidentally deleted.
Missing At Random (MAR)
- P depends on X, but not on Y.
- Example: Participants with higher age are less likely to respond to their political opinion.
Missing Not At Random (MNAR or NMAR)
- P depends on Y (and possibly on X).
- Example: Participants with higher incomes report their income less often.
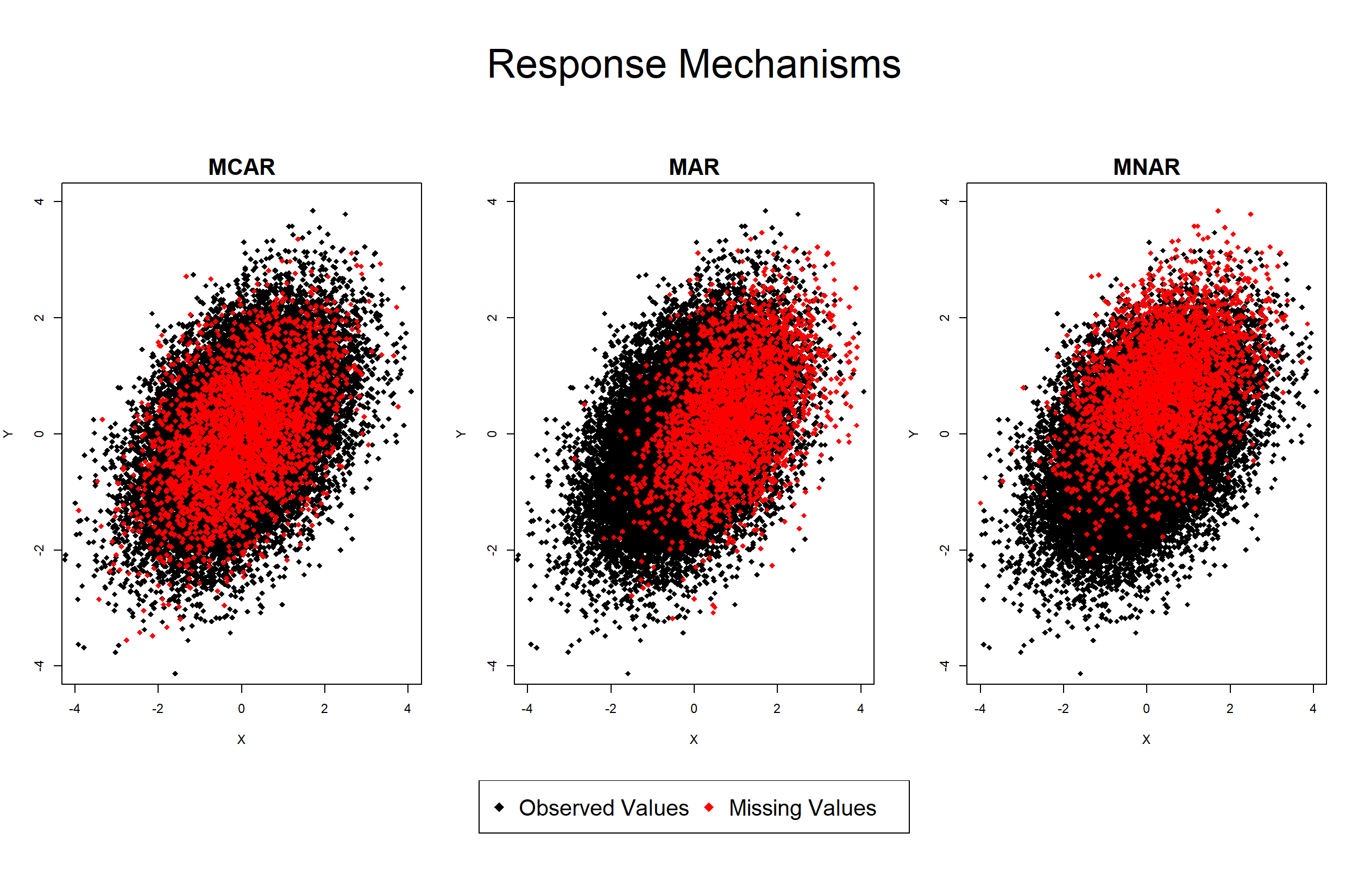
Graphic 1: Response Mechanisms MCAR, MAR, and MNAR
In Graphic 1 you can see an illustration of different types of incomplete data, i.e. response mechanisms.
The three panes of the graphic show the same correlation plot between the variables X and Y. However, each plot reflects a different response pattern – Observed values are shown in black; Missing values are shown in red.
The left plot illustrates the response mechanism Missing Completely At Random (MCAR).
As you can see, there is no significant difference between the distributions of observed and missing values (black and red are spread in the same way).
In this case, the missing values reduce our observed sample size, i.e. the variance of our estimations would be increased, but they do not lead to bias in our estimates.
If sample size is no major problem of our data set, we can deal with our incomplete data in many different ways, e.g. pairwise or listwise deletion. In case we want to preserve a bigger sample size, more sophisticated methods such as missing data imputation should be applied in order to deal with our missing values. Learn more about these methods in the next section of this article.
The response mechanism Missing At Random (MAR) is shown in the middle plot.
In this case, the red data points, i.e. the missing values, are located more often on the right side of the plot. In other words, individuals with a higher value in X are less likely to respond.
The structure of the red points is only determined by X, not by Y. Hence, the red points are shifted strongly to the right, but only slightly toward higher values of Y (due to the positive correlation of X and Y).
This is probably the most important point of response mechanism theory, so let’s emphasize this again:
Due to the positive correlation of X and Y, missing values are also shifted slightly upwards, i.e. toward higher values of Y, even though there is no direct influence of Y on the response propensity P.
For that reason, our missing data analysis and the resultant survey estimates of Y are likely to be biased, if we do not handle this type of incomplete data in an adequate way.
However, bias can be reduced by imputing missing cases on the basis of an appropriate imputation model.
The distribution of missing values changes in the right plot, which represents the response mechanism Missing Not At Random (MNAR/NMAR).
The missing values are strongly shifted toward higher values of Y and slightly toward higher values of X. It’s exactly the opposite as in the middle plot.
If nonresponse is MNAR, the response propensity P is directly influenced by Y and hence our analysis of Y is at risk to be highly biased.
It is possible (and also likely) that there are additional influences of X on P in case of MNAR. For illustration, however, this example consists only of an influence of Y on P.
The typically used methodology for handling missing data is, unfortunately, often not able to correct all bias that results from this response pattern.
Furthermore, in practice it is usually impossible to distinguish between MAR and MNAR, since we do not know how the missing cases are distributed.
Due to these reasons, practitioners often just assume that nonresponse is MAR – A fairly strong assumption.
However, due to a lack of (easily applicable) alternatives, this assumption is often the way how users deal with this issue in practice.
Handling Missing Values
There are many different ways how missing values can be handled and missing data research is constantly developing new methods for the analysis and treatment of missing data.
In the following, I give you an (incomprehensive) overview about several approaches for dealing with missing data.
Klick on the pictures on the left in order to get more information about methods and topics you are interested in.
Listwise Deletion for Missing Data
Listwise deletion (sometimes called casewise deletion or complete case analysis) is the default method for handling missing values in many statistical software packages such as R, SAS, or SPSS.
Listwise deletion is easy to apply, but the method has some drawbacks that you should consider when you have to deal with missing data.
In this post, I’m giving an introduction to the main concepts of listwise deletion, including examples in R and SPSS and a discussion about the legitimacy of listwise deletion.
Missing Data Imputation
Missing value imputation is one of the more sophisticated approaches for handling incomplete data.
To make it easier for you, I have prepared one introductory article about the general concept of missing data imputation and several subsequent articles with more detailed explanations and examples of different imputation methods.
In the subsequent articles, I cover the topics:
> Zero imputation
> Mean imputation
> Mode imputation
> Hot deck imputation
> Regression imputation
> Multinomial logistic regression imputation
> Predictive mean matching
> What is the most popular imputation method?
However, if you don’t know anything about missing data imputation yet, I recommend to read the
introductory article about imputation first.
Find Missing Values in R
An important precondition for dealing with missing data in R is the knowledge about how the missing values are distributed in your data.
In this article, I will show you how to find missing values with the programming software R.
I give several examples how to identify and investigate the structure of missing values in vectors, data frames, and matrices. The post also includes the handling of missing values in different variable classes, i.e. continuous and categorical variables.
Complete Cases in R (3 Examples)
The complete.cases function provides the possibility to scan your data for observed values.
In this article, I’m explaining how to use the complete.cases function of the R programming language in practice.
On the basis of 3 practical examples, I’m showing you how to
1) Find observed and missing values in a data frame
2) Check a single column or vector for missings
3) Apply the complete.cases function to a real data set
If you are interested in the handling of missing values in R, you may also be interested in this article about the is.na function. Furthermore, you may have a look at the following video that was published on the Data Professor YouTube channel. In the video, I explain how to handle missing values in R:
Why Missing Data Analysis is Important
If you want to learn more about the trouble with missing data and the importance of an appropriate statistical handling of missing values in your database, I can recommend the following video of the YouTube channel Computerphile.
In the video, Professor Uwe Aickelin speaks about troubles with missing values in modern data sets, the challenges of big data, interpretation of response mechanisms, and about whether there is a need to replace missing values in these kind of data.
Now It’s Your Turn!
I gave you an introduction into the concept of missing data and provided you with a bunch of ways to handle missing values.
Now I would like to hear from you!
What is your favorite way to deal with missing data? Are you using a simple listwise deletion or do you prefer more sophisticated methods such as missing data imputation?
Do you have any questions about missing data and the related methods? Let me know in the comments, I’m happy to answer all questions!
References
Little, R. J. A. and Rubin, D. B., editors (2002). Statistical Analysis with Missing Data. Wiley-Blackwell.
Templ, M., Alfons, A, Kowarik A., and Prantner B. (2017). Package VIM
Appendix
Appendix A: R Code for the header graphic of this page
library("VIM") # Load VIM package in RStudio # Create some example data set.seed(857632) # Set seed N <- 1000 # Sample size var1 <- NA # Some NA variables var2 <- NA var3 <- NA var4 <- rnorm(N) # Some random normally distributed variables var5 <- rnorm(N) var6 <- rnorm(N) var7 <- rnorm(N) var8 <- rnorm(N) var9 <- rnorm(N) var10 <- rnorm(N) var11 <- rnorm(N) var12 <- rnorm(N) var13 <- rnorm(N) var14 <- rnorm(N) var15 <- rnorm(N) var16 <- rnorm(N) var17 <- rnorm(N) var18 <- rnorm(N) var19 <- rnorm(N) var20 <- rnorm(N) var21 <- rnorm(N) var22 <- rnorm(N) var23 <- rnorm(N) var24 <- rnorm(N) var25 <- rnorm(N) var26 <- rnorm(N) var27 <- rnorm(N) var28 <- rnorm(N) var29 <- rnorm(N) var30 <- rnorm(N) var4[1:200] <- NA # Insert missings var5[1:175] <- NA var6[1:150] <- NA var7[1:125] <- NA var8[1:100] <- NA var9[50:200] <- NA var10[50:175] <- NA var11[50:150] <- NA var12[50:100] <- NA var13[100:200] <- NA var14[rbinom(N, 1, 0.05) == 1] <- NA # Some random missing values var15[rbinom(N, 1, 0.15) == 1] <- NA var16[rbinom(N, 1, 0.05) == 1] <- NA var17[rbinom(N, 1, 0.02) == 1] <- NA var18[rbinom(N, 1, 0.01) == 1] <- NA var19[rbinom(N, 1, 0.005) == 1] <- NA var20[rbinom(N, 1, 0.001) == 1] <- NA var21[rbinom(N, 1, 0.001) == 1] <- NA var22[rbinom(N, 1, 0.001) == 1] <- NA var23[rbinom(N, 1, 0.001) == 1] <- NA var24[rbinom(N, 1, 0.001) == 1] <- NA var25[rbinom(N, 1, 0.001) == 1] <- NA df_header <- data.frame(var1, var2, var3, var4, var5, # Create data frame var6, var7, var8, var9, var10, var11, var12, var13, var14, var15, var16, var17, var18, var19, var20, var21, var22, var23, var24, var25, var26, var27, var28, var29, var30) aggr(df_header, # Create aggregation plot bars = FALSE, col = c("royalblue3", "orangered"), border = "royalblue3", combined = TRUE)
Appendix B: R Code for Graphic 1: Response Mechanisms MCAR, MAR, and MNAR
set.seed(653) # Set seed in for reproducibility # Create example data N <- 30000 # Sample size of 30000 y <- rnorm(N) # y without any missing values x <- 0.5 * y + rnorm(N) # x correlated with y # Create missings according to the MCAR response mechanism MCAR_missings <- rbinom(N, 1, 0.1) == 1 # 10% of Y are set to missing # Missing values according to the MAR response mechanism x_normalized <- (x - min(x)) / (max(x) - min(x)) # Normalize x to 0-1 range x_normalized <- x_normalized^4 # x_normalized to the power of 4 # in order to make the values smaller MAR_missings <- rbinom(N, 1, x_normalized) == 1 # Use x_normalized as probability # that a missing value in Y occurs # Missingness according to the MNAR (or NMAR) response mechanism y_normalized <- (y - min(y)) / (max(y) - min(y)) # Normalize y to 0-1 range y_normalized <- y_normalized^4 # y_normalized to the power of 4 # in order to make the values smaller MNAR_missings <- rbinom(N, 1, y_normalized) == 1 # Use y_normalized as probability # that a missing value in Y occurs # Plot response mechanisms m <- matrix(c(1, 1, 1, 2, 3, 4, 5, 5, 5), # Set layout of graph nrow = 3, ncol = 3, byrow = TRUE) layout(mat = m, heights = c(0.1, 0.4, 0.1)) par(mar = c(4, 4, 2.2, 2)) plot.new() mtext("Response Mechanisms", # Shared title side = 3, line = - 3, cex = 2) plot(x[MCAR_missings == FALSE], # MCAR: Plot observed values of x and y y[MCAR_missings == FALSE], xlab = "X", ylab = "Y", main = "MCAR", pch = 18, cex.main = 1.75, xlim = c(- 4, 4), ylim = c(- 4, 4)) points(x[MCAR_missings], # MCAR: Plot missing values of x and y y[MCAR_missings], col = "red", pch = 18) plot(x[MAR_missings == FALSE], # MAR: Plot observed values of x and y y[MAR_missings == FALSE], xlab = "X", ylab = "Y", main = "MAR", pch = 18, cex.main = 1.75, xlim = c(- 4, 4), ylim = c(- 4, 4)) points(x[MAR_missings], # MAR: Plot missing values of x and y y[MAR_missings], col = "red", pch = 18) plot(x[MNAR_missings == FALSE], # MNAR: Plot observed values of x and y y[MNAR_missings == FALSE], xlab = "X", ylab = "Y", main = "MNAR", pch = 18, cex.main = 1.75, xlim = c(- 4, 4), ylim = c(- 4, 4)) points(x[MNAR_missings], # MNAR: Plot missing values of x and y y[MNAR_missings], col = "red", pch = 18) plot(1, type = "n", axes = FALSE, # Empty plot for legend xlab = "", ylab = "") legend(x = "top", inset = 0, # Shared legend legend = c("Observed Values", "Missing Values"), col = 1:2, pch = 18, cex = 1.7, horiz = TRUE)








12 Comments. Leave new
Short but full of practical knowledge, Awesome expression.
Thank you, it was very useful.
Thanks for the kind words Onur, I’m glad to hear that you liked it!
Thank you for your good content. Please why do they commonly used median or mean to replace missing value in R and Pandas when doing data analysis.
Hey Gude,
Thank you very much for the kind words!
regarding your question: I think in most cases it introduces bias when you are using mean or mode imputation. I recommend using more sophisticated methods such as predictive mean matching instead.
Regards,
Joachim
How about using Maximum Likelihood or Expectation-Maximization Techniques to handle the missing data?
Hey Umar,
I have never done this myself, but the mlmi package seems to provide functions for Maximum Likelihood Multiple Imputation in R.
Regards,
Joachim
Thank you. I have learned so many things from you. I have a question. Suppose
x <- 1:10
y <- c(3, NA, 1, NA, 3, NA, 9, NA, 2, NA)
df <- data.frame(x, y)
and I want to check whether my data is MAR, MCAR, or NMAR. How do I draw a response mechanism graph for my data?
Hi Saima,
Thank you so much for the kind words, glad to hear that!
I apologize for the delayed reply. I was on a long holiday, so unfortunately I wasn’t able to get back to you earlier. Do you still need help with your syntax?
Regards,
Joachim
yes
Hi Saima,
Unfortunately, this is very difficult in real life situations, since we do not know the true values of the missing data. You can test your data for MCAR using Little’s missing completely at random test (see here). However, this method does also have its drawbacks.
Regards,
Joachim
You are really a great statistician. Thanks.
Thank you so much for the kind words Saima, glad you think so!
Regards,
Joachim