Predictive Mean Matching Imputation (Theory & Example in R)
Predictive mean matching is the new gold standard of imputation methodology!
Forget about all these outdated and crappy methods such as mean substitution or regression imputation…
In the following article, I’ll show you why predictive mean matching is heavily outperforming all the other imputation methods for missing data.
I have split the article in several sections. You may jump to the specific topic you are interested in:
Predictive Mean Matching Explained
Before we can dive into the R programming example, let’s first define what predictive mean matching exactly is. The predictive mean matching algorithm can be split into 6 steps (See also Paul Allison or Vink et al., 2014):
- Estimate a linear regression model:
- Use the variable we want to impute as \(Y\).
- Use a set of good predictors as \(X\) (Guidelines for the selection of \(X\) can be found in van Buuren, 2012, p. 128).
- Use only the observed values of \(X\) and \(Y\) to estimate the model.
- Draw randomly from the posterior predictive distribution of \(\hat{\beta}\) and produce a new set of coefficients \(\beta^{*}\).
- This bayesian step is needed for all multiple imputation methods to create some random variability in the imputed values.
- More details, e.g., in Yuan, 2005.
- Calculate predicted values for observed and missing \(Y\).
- Use \(\hat{\beta}\) to calculate predicted values for observed \(Y\).
- Use \(\beta^{*}\) to calculate predicted values for missing \(Y\).
- For each case where \(Y\) is missing, find the closest predicted values among cases where \(Y\) is observed.
- Example:
- \(Y_i\) is missing. Its predicted value is 10 (based on \(\beta^{*}\)).
- Our data consists of five observed cases of \(Y\) with the values 6, 3, 22, 7, and 12.
- In step 3, we predicted the values 7, 2, 20, 9, and 13 for these five observed cases (based on \(\hat{\beta}\)).
- The predictive mean matching algorithm selects the closest observed values (typically three cases) to our missing value \(Y_i\). Hence, the algorithm selects the values 7, 9, and 13 (the closest values to 10).
- Draw randomly one of these three close cases and impute the missing value \(Y_i\) with the observed value of this close case.
- Example continued:
- The algorithm draws randomly from 6, 7, and 12 (the observed values that correspond to the predicted values 7, 9, and 13).
- The algorithm chooses 12 and substitutes this value to \(Y_i\).
- In case of multiple imputation (which I strongly advise), steps 1-5 are repeated several times.
- Each repetition of steps 1-5 creates a new imputed data set.
- With multiple imputation, missing data is typically imputed 5 times.
Predictive Mean Matching in R (Example)
I have to admit, the predictive mean matching algorithm is not so easy to understand, when you read it the first time. However, in practice it’s easy to apply!
In the following, I’m going to show you how to apply predictive mean matching in R.
Let’s create some random data for our example:
##### Example data ##### set.seed(918273) # Seed N <- 3000 # Sample size y <- round(runif(N, -10, 10)) # Target variable Y x1 <- y + round(runif(N, 0, 50)) # Auxiliary variable 1 x2 <- round(y + 0.25 * x1 + rnorm(N, - 3, 15)) # Auxiliary variable 2 x3 <- round(0.1 * x1 + rpois(N, 2)) # Auxiliary variable 3 x4 <- as.factor(round(0.02 * y + runif(N))) # Auxiliary variable 4 (categorical variable) y[rbinom(N, 1, 0.2) == 1] <- NA # Insert 20% missing data in Y data <- data.frame(y, x1, x2, x3, x4) # Store data in dataset head(data) # First 6 rows of our data
Our data consists of five variables: A target variable \(Y\) with 20% missing values and four auxiliary variables \(X_1\), \(X_2\), \(X_3\), and \(X_4\). The first six rows of our example data look as follows:
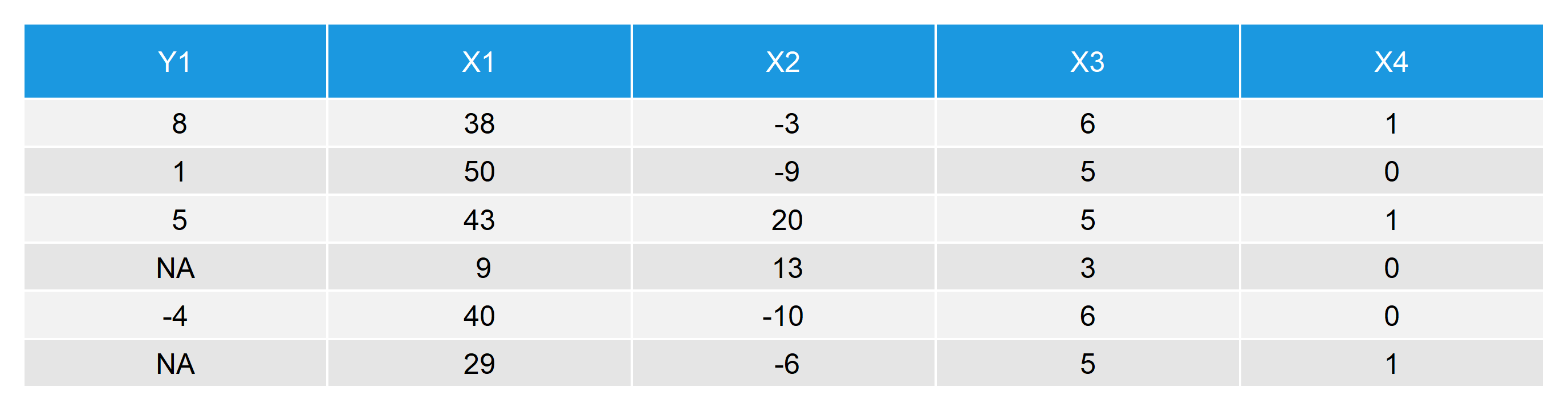
Table 1: First Six Rows of Our Data with Missing Values in Y
Let’s move on to the application of predictive mean matching to our example data. First, we need to install the R package mice (detailed explanations can be found in van Buuren and Groothuis-Oudshoorn, 2011).
##### Install mice package in R##### install.packages("mice") # Install mice package library("mice") # Load mice package
With the following code, we can impute our missing data via single imputation.
The function mice is used to impute the data; m = 1 specifies single imputation; and method = “pmm” specifies predictive mean matching as imputation method.
The function complete stores the imputed data in a new data object (in our example, we call it data_imp_single).
##### Impute data via predictive mean matching (single imputation)##### imp_single <- mice(data, m = 1, method = "pmm") # Impute missing values data_imp_single <- complete(imp_single) # Store imputed data # head(data_imp_single) # First 6 rows of our imputed data
As I mentioned previously, single imputation is almost never a good idea, since it underestimates your standard errors. However, by specifying m = 5 within the function mice, you can easily switch to multiple imputation (i.e. 5 imputed data sets).
The specifications “repeated” and include = TRUE tell the complete function how to store our multiply imputed data in the object data_imp_multi_all. Have a look at the documentation of complete in order to explore different ways of storing your imputed data (by typing ?complete into your R Studio console).
With the remaining code we do some simple data cleaning and store the dataset in the object data_imp_multi.
##### Predictive mean matching (multiple imputation)##### imp_multi <- mice(data, m = 5, method = "pmm") # Impute missing values multiple times data_imp_multi_all <- complete(imp_multi, # Store multiply imputed data "repeated", include = TRUE) data_imp_multi <- data.frame( # Combine imputed Y and X1-X4 (for convenience) data_imp_multi_all[ , 1:6], data[, 2:5]) head(data_imp_multi) # First 6 rows of our multiply imputed data
This is how our multiply imputed data set looks like:
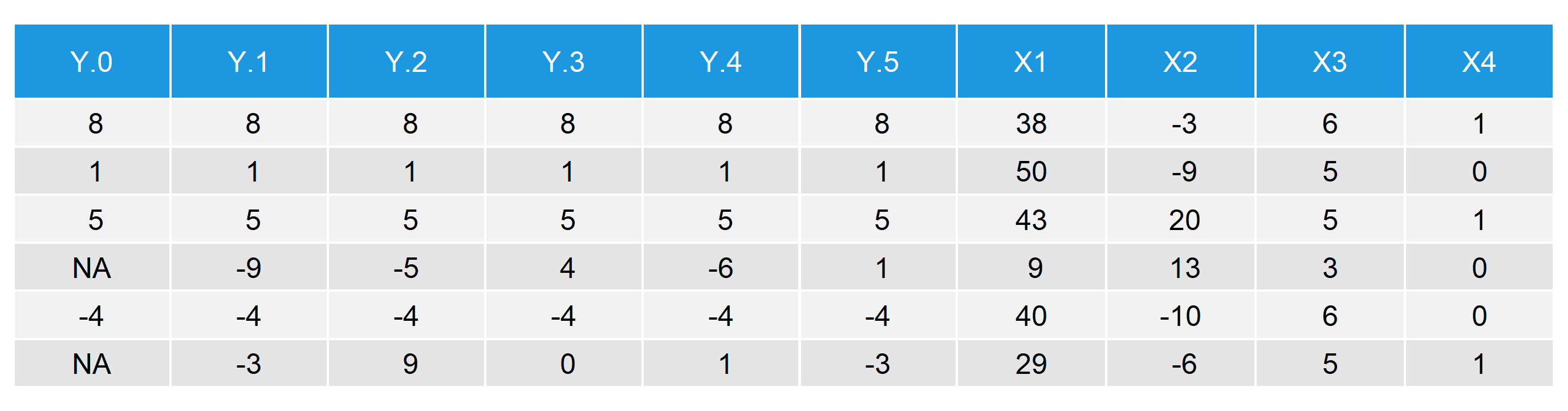
Table 2: First Six Rows with Multiply Imputed Values
- \(Y.0\) is equal to the original \(Y\) with missing values.
- \(Y.1\)–\(Y.5\) are the five imputed versions of \(Y\).
- \(X1\)–\(X4\) are the four auxiliary variables that we used as predictors for the imputation.
By comparing rows 4 and 6, i.e. the rows with NAs, you can see the effect of multiple imputation. While \(Y.0\) contains missings, \(Y.1\)–\(Y.5\) are filled with imputed values. Note that the imputed values differ between the five imputed data sets (row 4: -9, -5, 4, -6, 1; row 6: -3, 9, 0, 1, -3).
You might say: “Isn’t that bad?! It seems like the imputed values are very different to each other.”
Yes, they are different – But that is exactly what we expect (and what we want) when we do multiple imputation. The difference between the imputed values reflects the uncertainty of our imputation. When we calculate standard errors (i.e. confidence intervals) for our point estimates, we include this uncertainty into the calculation, which leads to more correct standard errors.
Predictive Mean Matching vs. Stochastic Regression Imputation
In a previous post, I discussed pros and cons of stochastic regression imputation. Regression imputation has many advantages, but I have also shown two serious drawbacks:
- Stochastic regression imputation might lead to implausible values (e.g. negative incomes).
- Stochastic regression imputation has problems with heteroscedastic data.
In my previous post, I raved about predictive mean matching, as this method is supposed to fix all the problems of regression imputation.
Of course I do not want to deprive you of the proof! Therefore, I’m going to use exactly the same data as in the regression imputation example – but this time I’m also imputing via predictive mean matching.
Plausibility of Imputed Values
Let’s have a closer look at drawback 1 – the plausibility of imputed values. Consider the following example data:
# Income data set.seed(91919) # Set seed N <- 1000 # Sample size income <- round(rnorm(N, 0, 500)) # Create some synthetic income data income[income < 0] <- income[income < 0] * (- 1) x1 <- income + rnorm(N, 1000, 1500) # Auxiliary variables x2 <- income + rnorm(N, - 5000, 2000) income[rbinom(N, 1, 0.1) == 1] <- NA # Create 10% missingness in income data_inc_miss <- data.frame(income, x1, x2)
We impute once via stochastic regression imputation…
imp_inc_sri <- mice(data_inc_miss, method = "norm.nob", m = 1) data_inc_sri <- complete(imp_inc_sri)
… and once via predictive mean matching (for the sake of simplicity, both times via single imputation).
imp_inc_pmm <- mice(data_inc_miss, method = "pmm", m = 1) data_inc_pmm <- complete(imp_inc_pmm)
Comparing the plausibility of both imputations, we can see that stochastic regression imputation leads to 10 implausible values (i.e. incomes below 0):
data_inc_sri$income[data_inc_sri$income < 0] # 10 values below 0 (implausible) # [1] -57.8859452 -58.9457388 -104.1099599 -147.9968026 -70.9192935 -280.2621111 # [2] -0.5694554 -91.3508690 -76.8628876 -468.5756297
Predictive mean matching, on the other hand, does not lead to implausible values:
data_inc_pmm$income[data_inc_pmm$income < 0] # No values below 0
In respect to the plausibility of imputed values, predictive mean matching clearly outperforms stochastic regression imputation.
Reason: Predictive mean matching only imputes values that were actually observed for other units. The range of imputed values therefore always lies between the minimum and the maximum of the observed values.
Imputation of Heteroscedastic Data
How well does predictive mean matching work for heteroscedastic data (i.e. drawback 2)? Let’s check it with the following example data:
# Heteroscedastic data set.seed(654654) # Set seed N <- 1:5000 # Sample size a <- 0 b <- 1 sigma2 <- N^2 eps <- rnorm(N, mean = 0, sd = sqrt(sigma2)) y <- a + b * N + eps # Heteroscedastic variable x <- 30 * N + rnorm(N[length(N)], 1000, 200) # Correlated variable y[rbinom(N[length(N)], 1, 0.3) == 1] <- NA # 30% missings data_het_miss <- data.frame(y, x)
As before, we first impute by stochastic regression imputation…
imp_het_sri <- mice(data_het_miss, method = "norm.nob", m = 1) data_het_sri <- complete(imp_het_sri)
… and then by predictive mean matching:
imp_het_pmm <- mice(data_het_miss, method = "pmm", m = 1) data_het_pmm <- complete(imp_het_pmm)
A good way for evaluating the two imputation methods for heteroscedastic data is a simple correlation plot:
par(mfrow = c(1, 2)) # Both plots in one graphic plot(x[!is.na(data_het_sri$y)], # Plot of observed values data_het_sri$y[!is.na(data_het_sri$y)], main = "", xlab = "X", ylab = "Y") points(x[is.na(y)], data_het_sri$y[is.na(y)], # Plot of missing values col = "red") title("Stochastic Regression Imputation", # Title of plot line = 0.5) abline(lm(y ~ x, data_het_sri), # Regression line col = "#1b98e0", lwd = 2.5) legend("topleft", # Legend c("Observed Values", "Imputed Values", "Regression Y ~ X"), pch = c(1, 1, NA), lty = c(NA, NA, 1), col = c("black", "red", "#1b98e0")) plot(x[!is.na(data_het_pmm$y)], # Plot of observed values data_het_pmm$y[!is.na(data_het_pmm$y)], main = "", xlab = "X", ylab = "Y") points(x[is.na(y)], data_het_pmm$y[is.na(y)], # Plot of missing values col = "red") title("Predictive Mean Matching", # Title of plot line = 0.5) abline(lm(y ~ x, data_het_pmm), col = "#1b98e0", lwd = 2.5) legend("topleft", # Legend c("Observed Values", "Imputed Values", "Regression Y ~ X"), pch = c(1, 1, NA), lty = c(NA, NA, 1), col = c("black", "red", "#1b98e0")) mtext("Imputation of Heteroscedastic Data", # Main title of plot side = 3, line = - 1.5, outer = TRUE, cex = 2)
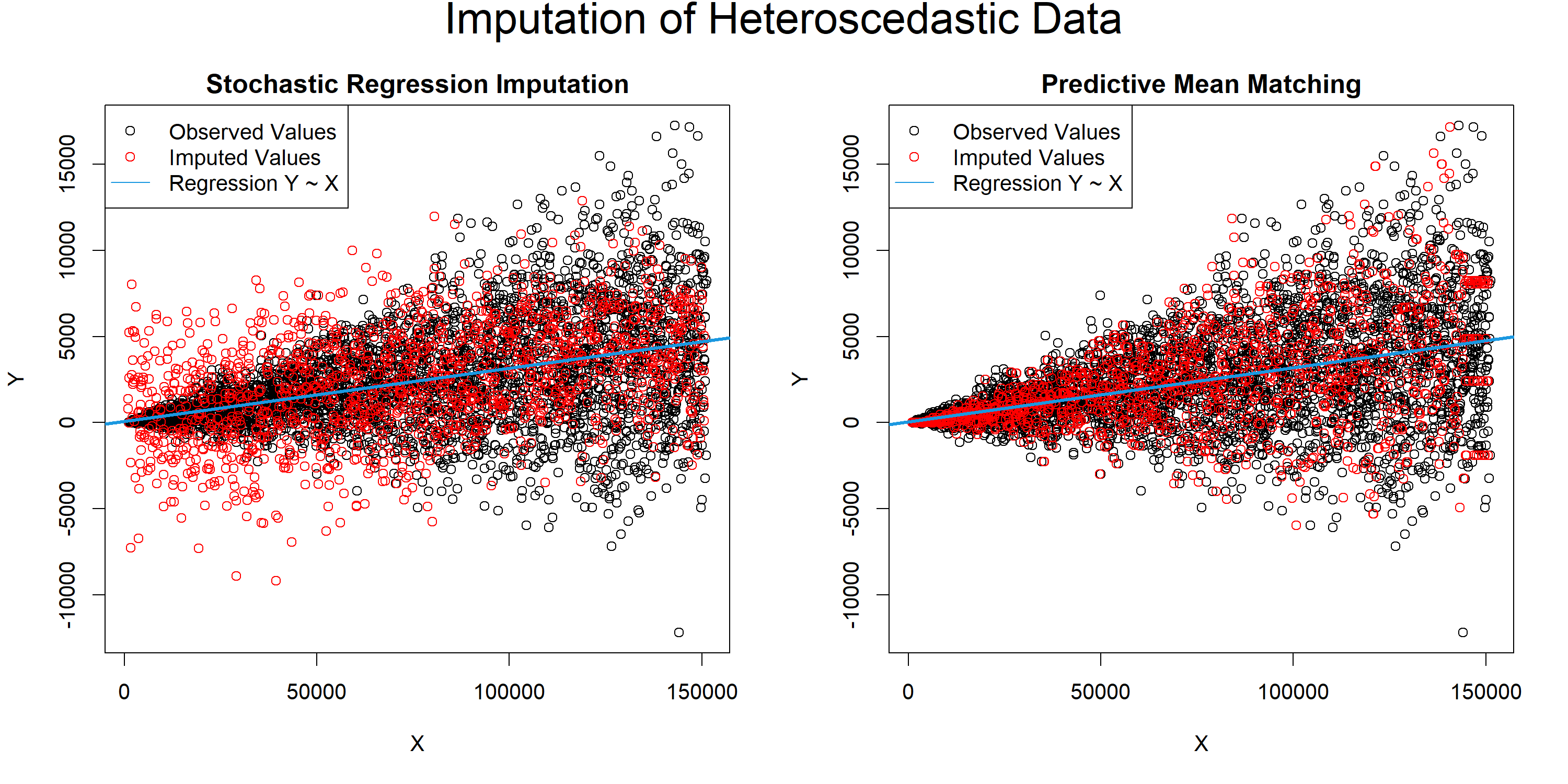
Graphic 1: Stochastic Regression Imputation vs. Predictive Mean Matching for Heteroscedastic Data
The plot makes it obvious:
Stochastic regression imputation overestimates the variance of smaller \(X\) and underestimates the variance of larger \(X\) – not good.
In contrast, predictive mean matching reflects the structure of our observed values almost perfectly – very good.
In other words: Even though stochastic regression imputation is much more popular among practitioners, there are strong arguments for using predictive mean matching instead!
PMM via Multiple Imputation in Stata (Video)
So far, I have only shown you how to apply predictive mean matching in R. However, the imputation method is implemented in many different software packages, such as SAS or Stata. Personally, I’m not an expert for these software packages, but there are many good instructions out there.
For instance, one tutorial I can recommend was published by the Stata YouTube channel. The speaker, Chuck Huber, explains step by step how to handle missing data by predictive mean matching in Stata.
I Would Like to Hear From You!
In this article, I have shown you why I’m such a big fan of predictive mean matching.
However, I would like to hear about your opinion!
Are you using predictive mean matching or do you prefer other imputation methods? Have I missed any pros or cons in my article?
Let me know in the comments (questions are also very welcome)!
References
van Buuren, S. (2012). Flexible Imputation of Missing Data. Chapman & Hall/CRC Interdisciplinary Statistics.
van Buuren, S., and Groothuis-Oudshoorn, K. (2011). mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software. 45(3).
Vink, G., Frank, L. E., Pannekoek, J., and van Buuren, S. (2014). Predictive mean matching imputation of semicontinuous variables. Statistica Neerlandica. 68(1). 61-90.
Yuan, C. Y. (2005). Multiple Imputation for Missing Data: Concepts and New Development. SAS Institute Inc., Rockville, MD.
Appendix
The header graphic of this page shows a correlation plot of two highly correlated variables. The black line indicates the regression slope. The black stars indicate missing values, which are replaced by a close observed value.
set.seed(123) # Seed N <- 50000 # Sample size x <- rnorm(N) # X variable y <- x + rnorm(N, 0, 1.5) # Y variable par(bg = "#353436") # Background color par(mar = c(0, 0, 0, 0)) # Remove space around plot plot(x, y, # Plot observed cases col = "#1b98e0", pch = 16, cex = 0.0001) abline(lm(y ~ x), # Plot regression slope lwd = 5, col = "#353436") points(x[1:30], y[1:30], # Plot missing cases col = "#353436", pch = 8, lwd = 2, cex = 3)
I’m Joachim Schork. On this website, I provide statistics tutorials as well as code in Python and R programming.
Statistics Globe Newsletter
Get regular updates on the latest tutorials, offers & news at Statistics Globe. I hate spam & you may opt out anytime: Privacy Policy.
52 Comments. Leave new
Please I help on how Gibbs sampling works in MICE
Hi Cynthia,
if you want to learn more about Gibbs sampling in MICE you could have a look at the book Flexible Imputation of Missing Data by Stef van Buuren. You can find a free PDF of the book here: http://pzs.dstu.dp.ua/DataMining/preprocessing/bibl/fimd.pdf
On page 86, he is explaining how Gibbs sampling is implemented in MICE.
Regards,
Joachim
Hello Sir Joachim,
Now that I already filled the missing values using imputation via predictive mean matching, what possible denoising method/s should be best used for my imputed dataset?
Hi Rosenel,
Denoising is usually not recommended after imputation with PMM because the method already preserves realistic variation, and removing that variation afterward can bias your results.
I hope this helps!
Joachim
hi,
According to your 6-step analysis, in the 3rd step,
–Use β∗ to calculate predicted values for missing Y,
I think you are saying that if the Y in ith sample (i.e., yi) is missing, then we could use x1i, x2i,…xni and β∗ to predicate the missing yi, so we need x1i,x2i…xni to predicate yi,
however, I find that , when I use mice in R, I still could get the predicated yi, even if the x1i, x2i,…xni are although missing. could you give me an explaination? thanks!
my data is like
Y X1 X2 X3 …. Xn
1 ob ob ob ob ob
2 ob ob ob ob ob
3 NA ob ob ob NA
…..
i NA NA NA NA NA (why the yi could be predicated?)
…
Hi Denghai,
this is because the MICE package is using a Multivariate Imputation by Chained Equations, i.e. missing values in predictors are also imputed. The following quote can be found in the help documentation of MICE:
“For predictors that are incomplete themselves, the most recently generated imputations are used to complete the predictors prior to imputation of the target column.”
Regards,
Joachim
Hello, I have a question.
I have a dataset with 40% missing value for one variable which its importance is relatively lower than other variables. I want to use this variable. so I applied pmm for this variable. (Other variables don’t have any missing value.) But, I have no idea to persuade my boss. Which one is better? (just remove this variable or apply pmm)
Hi Hwanwoo,
Usually, it is better to impute your data using PMM instead of deleting it. However, you may check whether your imputation model has a strong predictive power for the variable you want to impute, in order to check how good the imputation would be.
Regards,
Joachim
Hello,
Your post about PMM is really good and well written. It’s excellent because you add some comparison algorithm, to prove which one performs better. However, I have a question to ask. If I perform multiple imputations, how could I choose the value for the imputation if there is 5 value? should I go average 5 of the value instead, or is there any better approach?
Thank You.
Hi Alfin,
Thanks for the comment and the kind words. Glad to hear that you like the article! 🙂
Regarding your question: It is important to take the average of your multiple point estimates instead of the values themselves.
For example, if you want to estimate the mean of your five multiply imputed data sets, you would:
1) Estimate the mean five times.
2) Take the average of the five mean values.
I hope that helps!
Joachim
Thank you, it was very clear !
Thank you for the comment Marianne, glad to hear that you liked it!
Hi, thanks a lot for this post, it’s very clear and helpfull.
I have two questions :
1- Could you be more specific about the second step ? What do you mean when you say “Draw randomly from the posterior predictive distribution of β hat ” Is that a sampling like a MCMC method ?
2- When the predictors are incomplete how do we impute ? At wich step ?
Hi Odélia,
Thanks for the kind words!
1) This is the principle of Bayesian statistics. For more details, I recommend to have a look at the following Wikipedia page: https://en.wikipedia.org/wiki/Posterior_predictive_distribution
2) The imputation is circling around the data frame. As far as I know, the algorithm starts with the first column (please have a look at the documentation to make sure that this is correct). In other words: The missing values of the predictors are also imputed.
Regards,
Joachim
Hey there,
In the last step it says, that in multiple imputation, several imputed full data sets are created. How will these then be combined to one again? Does this depend on the type of the variable? (for example, the mean of all imputed missing values of the created sets when the variable is continuous, or the median if it is discrete?) Thanks you very much, finally understood how this works!
Best regards
Hey Lukas,
Thanks a lot for your comment and the nice words!
Regarding your question: Please have a look at Alfin Pradanas comment above. He had the same question like you 🙂
Let me know in case you need more explanations.
Joachim
Hello,
Thank you very much for sharing details about the methodology and syntax, it is very helpful! I am fairly new to using R and am reaching out to inquire if you can help clarify how I would specify the following within my code?
(I) I am wanting to use predicted mean matching to impute values for only 1 variable in my dataset. Am I able to indicate in the code to conduct the imputation on only 1 variable?
(II) I would like to match on a subset of variables in my dataset, am I able to specify specific variables to match on?
(III) Lastly, does your shared method assume that the missing mechanism is missing at random (MAR)?
Thank you very much for your time!
Kindly,
Adela
Hi Adela,
Thank you for the kind words! I’ll try to answer your questions below:
(I) In this case I would follow these steps: Create a data frame subset containing your target variable and all important predictors; Impute the entire subset; Replace the target variable in the original data frame with the imputed target variable.
(II) Could you explain what you mean with “match”? Do you mean you want to use only some variables as predictors? In this case you can either use the steps I have explained in (I), or you could use the predictorMatrix argument of the mice function.
(III) Yes, the method assumes MCAR or MAR. MNAR is more problematic.
Best regards,
Joachim
Thank you for the reply, Joachim, your responses are very helpful!
In follow-up to my second question about matching, does the method you explain find a value from the observed data that is close to the predicted value for replacement (rather than using the predicted values from the regression)?
Thank you again for your help.
Kindly,
Adela
I’m glad it helped!
Regarding your question: Yes this is correct. Predictive Mean Matching imputes observed values instead of predicted values (see 5. in the section “Predictive Mean Matching Explained”).
Regards,
Joachim
Thank you for confirming!
All the best,
Adela
You are welcome! 🙂
Hello!
I just wanted to thank you for taking the time to write this very helpful article. It’s unsung heroes like you that really help make scientific research a little better 🙂 I think I’m probably not the only non-data-scientist that felt there might be better ways to go about handling my missing values than listwise deletion, and by providing an introduction accessible to people like me we suddenly have an alternative that is practically feasible to learn!
Cheers,
Hey,
Thank you so much for this awesome feedback! It’s really great to hear that my tutorial helped to improve your statistical knowledge! 🙂
Regards
Joachim
Hey, Joachim!
First of all, loved what u wrote!
I’m a major student and I’m currently writing my thesis.
I have a problem that is the following:
I have a set of variables (one predictor and 22 response variables) and I have missing values in a lot of variables. My goal is to impute the missing values in the Y variable. The thing is that I’m not sure about the way to proceed given that the X variables also have missing values…can I do the multiple imputation on the Y variable in this conditions or do I need to get rid of the missing X’s variables values first? Can’t seem to find an answer for this anywhere.
Thank you so much!
Hey Ana,
Thanks a lot for the very kind feedback, glad you like the article!
Usually, I just impute all variables with missing values. This way you can use all rows of your data to impute the Y-variable.
An alternative would be to delete all rows with missing values in X. However, this may lead to bias in your imputation of the Y-variable, so I don’t recommend doing that.
I hope that helps!
Joachim
Thank you so much for this stunning explanation, this helped me a lot 🙂
Thank you very much for the kind comment Cylia, glad it was useful! 🙂
Thank you! This is a great article and the mice package looks super easy and slick
Thanks Soko, glad you find it helpful! Indeed, the mice package is great!
Regards,
Joachim
Thanks very much for the knwledge on how to fill in missing categorical data. However, I still have some difficulties filling multiple categorical columns with lots of missing categorical data. My data has about 21 categorical columns with 8 of these columns having missing values. Some of these columns can have up to 7 categories. I have tried different methhods to fill in the missing values to no success. Please, can you give me a helping hand using r? data source = https://www.kaggle.com/yasserh/loan-default-dataset
Hi Takum,
Please excuse the delayed response, I just came back from holidays. Are you still looking for help?
Regards,
Joachim
Dear Joachim,
Thanks for offering the tutorial. I think it may be helpful to mention that the variance of the imputed data. For example, you may run your models on the basis of the imputation. Then you may need to see the difference between different imputed datasets. Here you can use the variance to check the performance of the imputation.
All the best,
Shunqi
Hey Shunqi,
Thanks a lot for your hint! There are definitely many important methods that should be used to evaluate the imputation of missing values.
I think this goes beyond this specific tutorial, since I’m trying to focus on the predictive mean matching technique. However, evaluating the imputation output is something everybody should do in general.
Regards,
Joachim
how to calculate multiple linear regression?
Hey Alaa,
Do you want to use the regression for missing data imputation? In this case, you might have a look here.
Regards,
Joachim
When combining all the estimates obtained for each imputed dataset Could you also handle between and within variances of the imputation technique in R?
Hey Gilles,
Yes, this is possible. Please have a look at the documentation of the mice package (for example here), you will find functions for this task there.
Combining estimates from multiple imputations is referred to as “pooling” in this literature.
Best regards,
Joachim
Sir,
I want to know regarding missing valueT ,. I had to find relationship between bacterial richness and soil carbon. I have five sites. I collected the five samples from each site for soil variable. But for bacterial richness, the number of soil samples were different from each site because each site has different plant species, not exclusively but some were same. For example, site 1 has three plant species, thus collected have 9 samples, 3 replicates from each plant species. Now, I need to know how soil carbon vary with bacterial richness. I applied linear regression using stat_corr function “spearman”. Is it ok?
Hi Abdul,
It’s difficult to say without seeing your data, and I’m not an expert in this topic. However, Spearman correlation is reasonable for assessing a monotonic relationship. A concern is the varying sample sizes across sites, which could introduce bias. If soil carbon and bacterial richness are measured at different levels (e.g., site vs. plant species), a mixed-effects model might be more appropriate. Also, ensure your data meet correlation assumptions.
I hope this helps!
Regards,
Joachim
Where can I show you my data? I want to send it at your email address. Please share with me your email address. I have very little time left to submit my manuscript. Yours sincerely
Hey Abdul,
I run a Facebook discussion group where people can ask questions about R programming and statistics. Could you post your question there? This way, others can contribute/read as well: https://www.facebook.com/groups/statisticsglobe
For more detailed, personalized assistance, you may also take a look at our consulting page: https://statisticsglobe.com/consulting
Regards,
Joachim
Hey, Joachim!
First off, I just want to say—I absolutely loved what you wrote! It was so well-crafted and engaging.
I have some questions :
Subj id A B C D E
1 NA 60 M Yes NA
2 5 NA F No NA
3 NA NA M NA 452
4 8 84 M Yes 842
5 NA NA NA NA NA
“My target column is A, and I want to impute its missing values using Predictive Mean Matching (PMM).
1. Since other columns (B, C, D, E) also have missing values, do I need to impute them as well, or just focus on column A?
2. In the code, do I need to specify that A is the target variable and the others are predictors using a predictor matrix?
3. For Subject ID 5, where all values are missing, will imputation work correctly?
4. For categorical variables like Yes/No and M/F, do I need to convert them into numerical codes before imputation?
5. After generating 5 imputed datasets for A, I plan to take the average of the 5 imputed values (row wise) for each subject and use that as the final imputed values for A. Is this the correct approach?”
Hi Mahesh,
Thank you so much for the very kind words, glad you like my tutorial!
Regarding your questions:
1. Yes, you also have to impute them. This is automatically done in mice.
2. No, mice automatically imputes all variables.
3. I would remove this row as it doesn’t contain any information.
4. No, you can keep them as categorical (make sure to convert them to the factor class). mice will use other imputation methods suitable for this type of data by default.
5. The correct approach is to calculate your estimates five times and then take the average of these estimates. You can find more information here.
I hope this helps!
Regards,
Joachim
Hey Joachim, I really appreciate your help with my previous questions. I have one more doubt and would love your guidance.
For eg.
Y1 Y2 Y3 Y4 Y5 Final_Imputed
5 3 2 1 1 2.4
1 2 3 4 3 2.6
We are using the Predictive mean matching method (PMM) using the MICE Package in R.
I want the final dataset for analysis.
We took the imputed values from five datasets (Y1, Y2, Y3, Y4, Y5) for the same parameter and calculated the final imputed value by averaging them. For example, (5+3+2+1+1) ÷ 5 = 2.4.
We repeated this for all values and used the final imputed column for analysis.
Is this method correct or should we use a different approach ?
( If there are any other methods, please suggest their names briefly. )
You are welcome, glad it’s useful! Regarding your question, this is what I explained in 5. in my previous response:
5. The correct approach is to calculate your estimates five times and then take the average of these estimates. You can find more information here.
The method you are looking for is to “pool” the imputed data sets, see figure 1 in the link above.
Regards,
Joachim
Hi Joachim,
I saw your post in LinkedIn and tried to comment but comment field was detective.
I generated the data as similar like that pho you shared in your posts and reproduce the same results using PMM via pythonic package ‘miceforest’ with this GitHub Repo: https://github.com/AnotherSamWilson/miceforest
I create an issue in their repo to see what is the best practice and some hyper-parameters I need to use for real example like continues missing records (gap) you can check it out here: https://github.com/AnotherSamWilson/miceforest/issues/97
Let me know if you check the issue including notebook and if you has some tips for setup to improve the PMM results.
Hi Mario,
Thanks for the interesting comment. I’m glad my post inspired you to create this!
I can’t say much about the Python code, as I usually use R for imputing missing data. However, I had a look at your graph with imputed values, and I’d say it looks good.
Regards,
Joachim
Merci pour cet belle article.
J’aimerais savoir si c’est possible d’imputer les valeur manquante sur la meme colonne c’est à dire on se base sur les valeur qui se trouve sur la meme colonne pour imputer les valeurs manquantes.
Merci
Hi Abass,
Thanks for your kind comment.
If I understand your question correctly, then yes. Predictive mean matching does exactly that by using observed values from the same column as donors for the missing ones.
I hope this helps!
Joachim
Hi Joachim,
I’ve never heard of PMM so this was a nice introduction. Thank you! I feel like I might be missing something here. If this works so well, why might one go through the trouble of modeling? Suppose, income is my target variable. I split my data into train, validate, and test sets. Fit a random forest, so and so forth to predict income.
1) Why go through this hassle if I can just use PMM?
2) Is it safe to assume that the target variable and our set of predictors need to be associated in some way? The lack of auxiliary variables has resulted in poor propensity to respond models and predict income. This seems simple.
Hi Nirudika,
Thanks for your questions. I’m glad the introduction to PMM was helpful.
Regarding your first question, predictive mean matching is designed for imputing missing values, not for building predictive models. The idea is that a regression model is first used to compute predicted values, and then observations with similar predicted values are identified. One of their observed outcomes is then used as the imputed value. This works well for replacing missing values because it preserves realistic values from the dataset. However, PMM does not produce a model that can be used to predict outcomes for new observations. Methods such as random forests are used when the goal is to build a predictive model that generalizes to new data.
For your second question, yes, it is generally important that the predictors are associated with the variable that has missing values. If the predictors are weakly related to that variable, the imputation model will have little information to work with and the quality of the imputations may be poor. Including variables that are associated with the variable being imputed and with the missingness mechanism usually improves the imputation results.
Best regards,
Joachim