k-fold Cross-Validation in R (Example)

In this tutorial, you’ll learn how to do k-fold cross-validation in R programming. We show an example where we use k-fold cross-validation to decide for the number of nearest neighbors in a k-nearest neighbor (kNN) algorithm. We give you a general introduction into cross-validation here. The post has the structure:

Let’s get started!

Example Data & Add-On Packages

Install and load the class, caret, and data.table package.

install.packages("class")                             # Install & load class
library("class")
 
install.packages("data.table")                        # Install & load data.table
library("data.table")
 
install.packages("caret")                             # Install & load caret
library("caret")

Note that for the data.table package, we have an extra blog post here.

We create some example data. For the generation, we use a binomial logistic regression model, an extensive description of which can be found in Agresti (2012) Categorical Data Analysis.

N <- 50                                               # Number of observations
set.seed(888)                                         # Seed for reproducible results
X <- data.table(rnorm(N, mean = 2, sd = .5), rnorm(N, mean = 2, sd = .5),  # Create some auxiliary information
                rnorm(N, mean = 2, sd = .5), rnorm(N, mean = 2, sd = .5))
X_mod_mat <- model.matrix(~., X)                      # Create model.matrix from auxiliary information
beta_vec <- c(0, rep(1, 2), rep(-1, 2))               # Set beta coefficients
 
probs <- 1 / ( 1 + exp(- X_mod_mat %*% beta_vec) )    # Calculate class probabilities according to binary logistic regression model
round(quantile(probs), 3)                             # See the quantiles of the generated probabilities
#    0%   25%   50%   75%  100% 
# 0.067 0.281 0.454 0.610 0.889 
 
y <- factor(rbinom(n = N, size = 1, prob = probs))    # Draw concrete classes form the probabilities
prop.table(table(y)) * 100                            # Table the generated classes
# y
#  0  1 
# 54 46

Have a look at the previous output of the RStudio console. It shows that we generated a vector y with two classes from some generated auxiliary information X by use of a binary logistic regression model.

Example: K-Fold Cross-Validation With K-Nearest Neighbor

We take the generated data from above as given and want to use k-nearest neighbor (kNN) to predict whether new observations should be classified as 1 or 0 based on their auxiliary information X. For example, we might aim for imputing missing information with kNN, as explained in our blog post here.

For kNN, we have to decide for k, the number of nearest neighbors. We can use k-fold cross-validation to estimate how well kNN predicts new observation classes under different values of k. In the example, we consider k = 1, 2, 4, 6, and 8 nearest neighbors.

kNN_choices_k <- c(1, 2, 4, 6, 8)                     # Number of nearest neighbors to consider

We normalize the x variables for kNN.

X_norm <- X[, lapply(.SD, function (x) { ( x - min(x) ) / ( max(x) - min(x) ) }), # Normalize the data
            .SDcols = colnames(X)]

For k-fold cross-validation, we have to decide for a number of folds k. In this example, we take k=5 folds. That is, we want to conduct 5-folds cross-validation. Accordingly, you can change k for 3 or 10 to get 3-folds cross-validation or 10-fold cross-validation. Play around with the number of folds to get an impression of the number of folds suitable for your data at hand.

k_folds <- 5                                          # Number of folds in k-fold cross-validation

For k-fold cross-validation, we randomly subset our data in k folds of roughly equal size.

ind_train <- factor(sample(x = rep(1:k_folds, each = N / k_folds),  # Sample IDs for training data
                           size = N))
table(ind_train)                                      # Fold sizes
# ind_train
#  1  2  3  4  5 
# 20 20 20 20 20

You can see that there are 20 observations in each fold. We also have a more general post about splitting data in training and test data here.

Now, we do k-fold cross-validation with the following code. We do the following for all 5 folds: We consider the fold as the validation data and the rest k-1 folds as the training data. Based on the training data, we conduct a kNN algorithm with the different candidate neighbors. To see how well kNN works with the specified number of neighbors, we calculate the confusion matrix of the predictions of kNN on the validation set (our k-th fold). From the confusion matrix, we calculate the accuracy of the predictions as a measure indicating how well kNN predicts new observations.

out <- sapply(1:k_folds,                              # Apply k-fold cross-validation
              function (k_folds_i) {
 
                IDs <- ind_train == k_folds_i
 
                out_1 <- sapply(kNN_choices_k,        # For each number of nearest neighbors k: Calculate kNN
                                function (kNN_k_i) {
 
                                  model <- class::knn(train = X_norm[!IDs, ],
                                                      test  = X_norm[IDs, ],
                                                      cl    = y[!IDs],
                                                      k     = kNN_k_i)
 
                                  confMat <- caret::confusionMatrix(reference = y[IDs],  # Calculate confusion matrix
                                                                    data      = model,
                                                                    mode      = "everything")
 
                                  confMat$overall["Accuracy"]       # Return accuracy
 
                                })
 
                names(out_1) <- paste0("k_", kNN_choices_k)
                out_1
              })
colnames(out) <- paste0("fold_", 1:k_folds)
round(out, digits = 2)                                # Print output

Table 1 shows the results of the previous code. For each fold, we have the accuracy value achieved under the different integers of nearest neighbors (1, 2, 4, 6, 8). You can see that the values differ between different folds due to the variance in the data and the small number of observations.

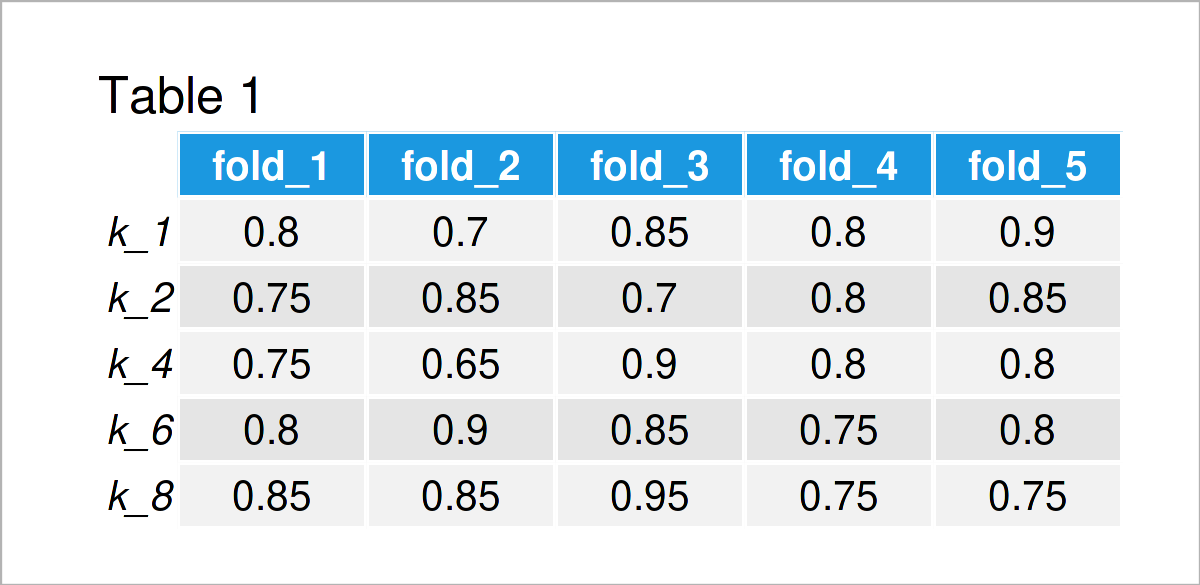
We take the mean value of the fold-specific accuracy scores to receive an overall estimate of how well the kNN generalizes to out-of-sample data under different values of k.

rowMeans(out)                                         # Mean values over k folds
#  k_1  k_2  k_4  k_6  k_8 
# 0.81 0.79 0.78 0.82 0.83

In this small example, kNN with 8 nearest neighbors performs best. Try the code above with other seeds, other candidate values for the number of nearest neighbors and different numbers of k-folds!

Video & Further Resources

I have recently released a video tutorial on the Statistics Globe YouTube channel, which illustrates the R programming code of this article. You can find the video below.

The YouTube video will be added soon.

Besides the video, you could have a look at the related tutorials on my homepage. A selection of posts can be found below:

• Mean Imputation for Missing Data (Example in R & SPSS)
• Regression Imputation (Stochastic vs. Deterministic & R Example)
• Predictive Mean Matching Imputation (Theory & Example in R)
• All R Programming Examples

At this point, you should know how to perform k-fold cross-validation in the R programming language. If you have additional questions, please tell me about it in the comments.

This page was created in collaboration with Anna-Lena Wölwer. Have a look at Anna-Lena’s author page to get further information about her academic background and the other articles she has written for Statistics Globe.