Loading Plot Explained (Example)

In this tutorial, I’ll illustrate explain what loading plot (also known as correlation circle) is and how it is used in Principal Component Analysis (PCA).

The article contains the following contents:

Let’s start!

Loading Plot

A loading plot is a visualization tool in PCA that shows the relationship between original variables and the first two or more principal components. In loadings plot, each variable’s loadings are represented by vectors, with the graph axes corresponding to the principal components.

The projection of a loading vector onto a principal component axis signifies the variable’s loading associated with that specific component. Consequently:

• The length of a variable’s projection onto an axis (e.g., PC1 or PC2) indicates its contribution to that principal component. A longer projection means a stronger influence on that component.
• Vectors with small angles in between have similar projections onto the principal component axes, indicating similar contributions.
• Vectors in nearly opposite directions have opposing projections, indicating opposite contributions.
• Orthogonal vectors have differing contributions to the principal components, especially when considering their projections onto the secondary axis (e.g., PC2 when observing PC1).

This geometric representation in loading plots provides a clear insight into the relationships among variables and their connections to the principal components, thereby enhancing our comprehension what the principal components represent.

Let’s next interpret a loading plot together!

Example

In this section, we will first use a loading plot to interpret the relationships among the variables in the iris dataset and their associations with the first principal components. Subsequently, we will smoothly explore what the principal components signify.

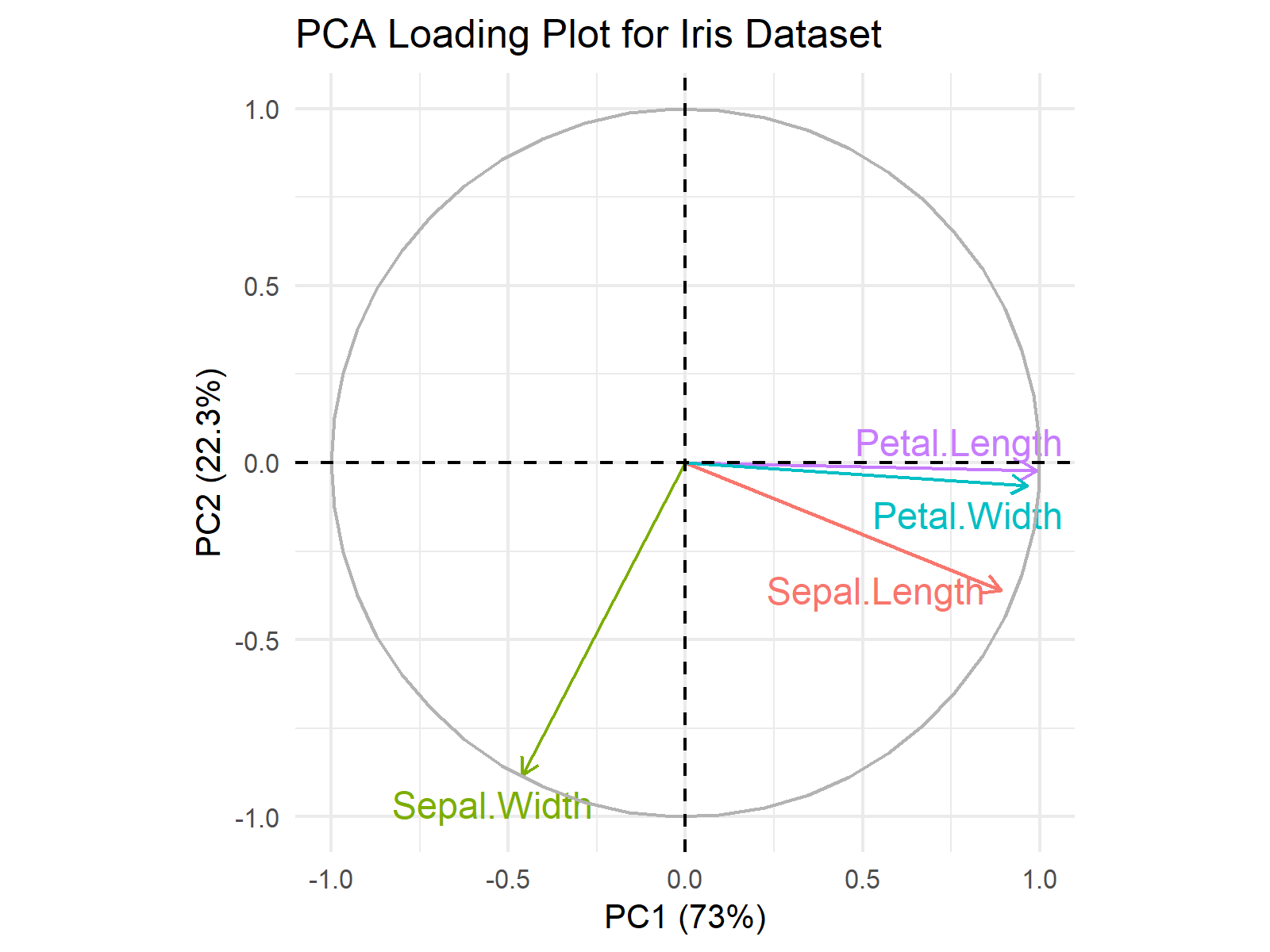
At first glance, the loading vectors for Petal.Width and Petal.Length closely align in a similar direction, resulting in comparable projections onto PC1 and PC2. This alignment implies a strong relationship between these two variables, as both contribute positively to PC1.

Conversely, Sepal.Length and.Sepal Width exhibit distinct contributions, separated by an angle of approximately 90 degrees. When considering their projections, it becomes evident that they have opposing contributions to PC1 while sharing similar contributions to PC2, where both variables negatively impact the component. However, it’s noteworthy that Sepal.Width contributes more significantly to PC2 compared to Sepal.Length.

Based on the observed relationships between the original variables and the principal components, we can conclude that PC1 represents a combination of smaller sepal widths and larger sepal lengths, while PC2 reflects lower measurements across all attributes, albeit at varying levels for each width and length measurement.

Do you agree with this interpretation of the principal components? If you have different insights, please share them in the comments.

Video, Further Resources & Summary

Have a look at the following video on my YouTube channel. I demonstrate the concept of this tutorial in the video:

In addition, you might want to read some of the other tutorials on our website. A selection of tutorials is listed below:

• What is Principal Component Analysis (PCA)?
• What are Loadings in PCA?
• Visualization of PCA in R
• Biplot for PCA Explained
• Advantages & Disadvantages of Principal Component Analysis

This tutorial has illustrated how to interpret loading plots. Please let me know in the comments section, in case you have further questions.

This page was created in collaboration with Cansu Kebabci. Have a look at Cansu’s author page to get more information about her professional background, a list of all his tutorials, as well as an overview on her other tasks on Statistics Globe.