Extract Standard Error, t-Value & p-Value from Linear Regression Model in R (4 Examples)

This post illustrates how to pull out the standard errors, t-values, and p-values from a linear regression in the R programming language.

The article consists of this information:

1) Creation of Example Data

2) Example 1: Extracting Standard Errors from Linear Regression Model

3) Example 2: Extracting t-Values from Linear Regression Model

4) Example 3: Extracting p-Values of Predictors from Linear Regression Model

5) Example 4: Extracting p-Value of F-statistic from Linear Regression Model

6) Video, Further Resources & Summary

Let’s just jump right in…

Creation of Example Data

First, we need to create some example data:

set.seed(1234421234)                       # Drawing randomly distributed data
x1 <- round(rnorm(1500), 2)
x2 <- round(rnorm(1500) - 0.1 * x1, 2)
x3 <- round(rnorm(1500) + 0.1 * x1 - 0.5 * x2, 2)
x4 <- round(rnorm(1500) - 0.4 * x2 - 0.1 * x3, 2)
x5 <- round(rnorm(1500) + 0.1 * x1 - 0.2 * x3, 2)
x6 <- round(rnorm(1500) - 0.3 * x4 - 0.1 * x5, 2)
y <- round(rnorm(1500) + 0.5 * x1 + 0.5 * x2 + 0.15 * x3 - 0.4 * x4 - 0.25 * x5 - 0.1 * x6, 2)
data <- data.frame(y, x1, x2, x3, x4, x5, x6)
head(data)                                 # Showing head of example data
#       y    x1    x2    x3    x4    x5    x6
# 1 -2.16 -0.15 -2.07  0.47  0.27 -0.62 -2.55
# 2  1.93  0.53  0.44  0.15 -0.53 -0.30  0.05
# 3 -0.34 -0.55 -0.63  1.94  0.56 -0.66  1.33
# 4 -0.37  1.81  0.20  0.13  1.10  0.76  0.50
# 5  0.37 -0.35  0.93 -1.43  0.65 -0.58 -0.19
# 6  1.74  1.68  1.61 -0.63 -3.16 -0.21  0.31

As you can see based on the previous RStudio console output, our example data is a data frame containing seven columns. The variable y is our target variable and the variables x1-x6 are the predictors.

Let’s fit a linear regression model based on these data in R:

mod_summary <- summary(lm(y ~ ., data))    # Estimate linear regression model
mod_summary                                # Summary of linear regression model

standard errors, t-values and p-values of linear regression model r

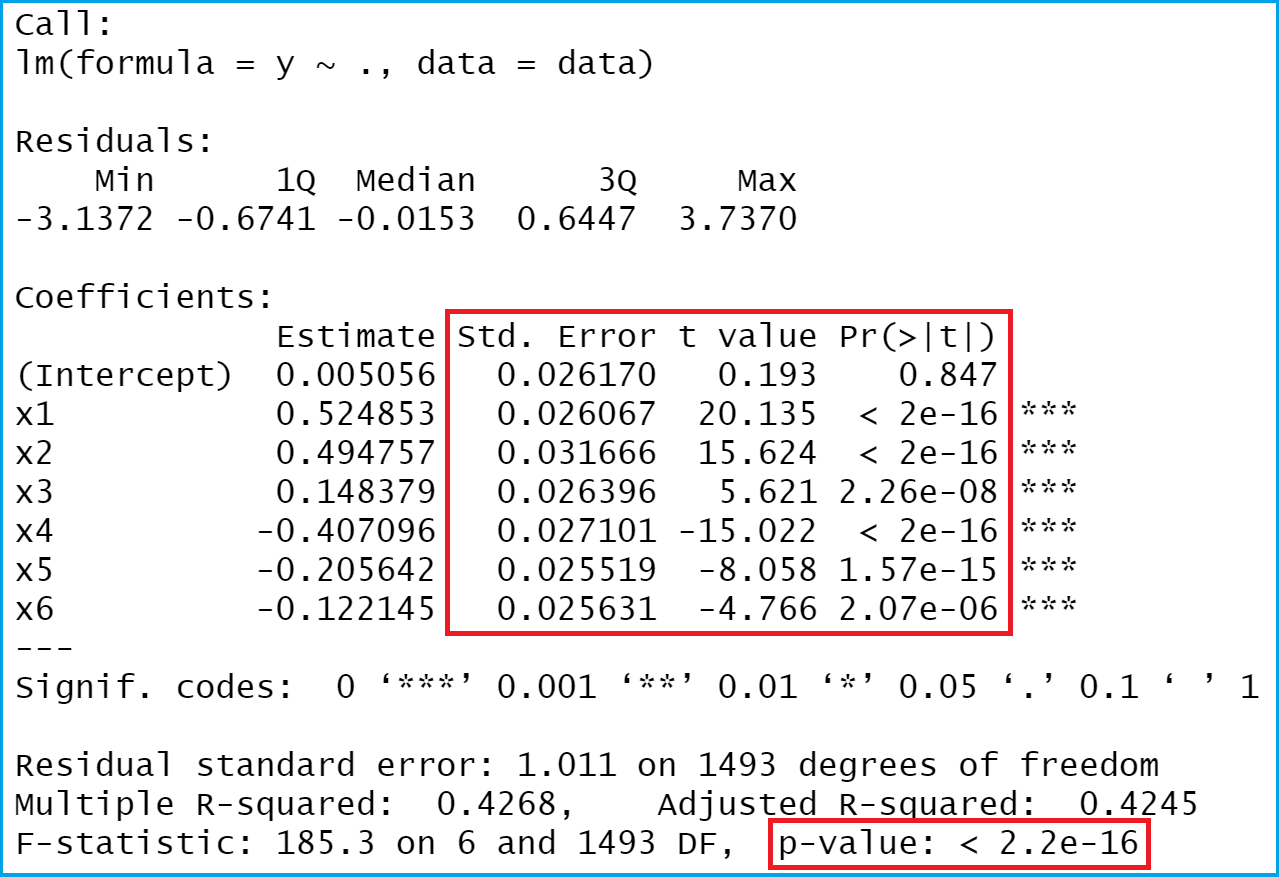
As you can see in Figure 1, the previous R code created a linear regression output in R. As indicated by the red squares, we’ll focus on standard errors, t-values, and p-values in this tutorial.

Let’s do this!

Example 1: Extracting Standard Errors from Linear Regression Model

This Example explains how to extract standard errors of our regression estimates from our linear model. For this, we have to extract the second column of the coefficient matrix of our model:

mod_summary$coefficients[ , 2]             # Returning standard error
# (Intercept)          x1          x2          x3          x4          x5          x6 
#  0.02616978  0.02606729  0.03166610  0.02639609  0.02710072  0.02551936  0.02563056

The output of the previous R syntax is a named vector containing the standard errors of our intercept and the regression coefficients.

Example 2: Extracting t-Values from Linear Regression Model

Example 2 illustrates how to return the t-values from our coefficient matrix.

mod_summary$coefficients[ , 3]             # Returning t-value
# (Intercept)          x1          x2          x3          x4          x5          x6 
#   0.1932139  20.1345274  15.6241787   5.6212606 -15.0215850  -8.0582917  -4.7656111

Again, the output is a named vector containing the values of interest.

Example 3: Extracting p-Values of Predictors from Linear Regression Model

Similar to the code of Example 2, this example extracts the p-values for each of our predictor variables.

mod_summary$coefficients[ , 4]             # Returning p-value
#  (Intercept)           x1           x2           x3           x4           x5           x6 
# 8.468177e-01 5.866428e-80 4.393611e-51 2.258705e-08 1.325589e-47 1.569553e-15 2.066174e-06

The previous result shows a named vector containing the p-values for our model intercept and the six independent variables.

Example 4: Extracting p-Value of F-statistic from Linear Regression Model

Be careful! The output of regression models also shows a p-value for the F-statistic. This is a different metric as the p-values that we have extracted in the previous example.

We can use the output of our linear regression model in combination with the pf function to compute the F-statistic p-value:

pf(mod_summary$fstatistic[1],              # Applying pf() function
   mod_summary$fstatistic[2],
   mod_summary$fstatistic[3],
   lower.tail = FALSE)
# 2.018851e-176

Note that this p-value is basically zero in this example.

Video, Further Resources & Summary

Do you want to learn more about linear regression analysis? Then you may have a look at the following video of my YouTube channel. In the video, I explain the R code of this tutorial in a live session.

The YouTube video will be added soon.

Besides the video, you may have a look at the other tutorials of this homepage:

In summary: At this point you should know how to return linear regression stats such as standard errors or p-values in R programming. Don’t hesitate to let me know in the comments section, in case you have further questions.

10 Comments. Leave new

Ludvig Ost
November 4, 2021 5:01 pm

How do I extract t-values from Linear Regression Model with multiple lms? To run the regression I use cbind for all the 9 dependent variables, like this:
fit <- lm(cbind(Y1, Y2, Y3, Y4, Y5, Y6, Y7, Y8, Y9) ~ X1 + X2 + X3, data = df).

Now I want to extract the t-values, unfortunately I only get error or "NULL". Please help me

Reply
- Joachim
  November 5, 2021 8:05 am
  
  Hey Ludvig,
  
  Could you illustrate how the output of this looks like? What happens when you print the fit object to the RStudio console, and what happens when you apply summary(fit) ?
  
  Regards,
  Joachim
  
  Reply

Ludvig Ost

November 5, 2021 9:59 am

When I print the fit object I get the intercept (alpha) and the slope (beta) of each X-value, for each dependent variable, ie 9 columns with alpha, slope X1, slope X2 and slope X3.

When I apply summary(fit) I get 9 regression outputs, including all the summary statistics like residuals, coefficients (estimate, std error, t-value, p-value) as well as r-squared and adj r-squared.

When I extracted the r-squared I used the lapply function, like this:
lapply(summary(fit),”[[“,”r.squared”), and ended up with a list of 9 r-squared values which I converted to a numeric object before making a data frame of it.

When I use the same code trying to extract t-values (lapply(summary(fit),”[[“,”t value”)) I get the same output, but no values, only “NULL”. I have also tried this code: lapply(fit, function(fit) summary(fit)$coefficients[,”t value”]) , but end up with this error code: Error in summary(fit)$coefficients :
$ operator is invalid for atomic vectors.

In the end I want a data frame consisting of alphas, r-squared values and t-values for all of my alphas. The only thing I miss is the latter.

Regards,
Ludvig

Joachim

November 6, 2021 6:47 am

I have created a reproducible example that extracts the t-values for each of the regression models. Please have a look at the following R code:

set.seed(396784)
df <- round(as.data.frame(matrix(rnorm(120), ncol = 12)), 1)
colnames(df) <- c("Y1", "Y2", "Y3", "Y4", "Y5", "Y6", "Y7", "Y8", "Y9", "X1", "X2", "X3")
df
#      Y1   Y2   Y3   Y4   Y5   Y6   Y7   Y8   Y9   X1   X2   X3
# 1   0.9 -1.0  1.7 -0.2  1.1  0.2  1.7  0.3  0.7  1.4 -1.1 -0.1
# 2  -1.6  0.7  0.1  1.4  0.0 -0.3  1.3 -0.6  1.6 -0.7 -0.6 -1.2
# 3   1.3 -0.6 -1.5  0.4  1.8 -1.3  0.2  2.1  0.5  0.6  0.6 -0.2
# 4   1.0 -0.2 -0.4  0.9  0.1  0.2  1.2 -0.3 -0.7  0.0  0.3 -0.3
# 5   0.4 -1.7  0.1  0.7 -1.6 -0.8 -0.8  0.7  0.4  0.7  0.4  1.1
# 6  -0.9 -0.1 -1.3 -0.2 -1.6  0.1  0.3 -0.1  0.5 -0.2  1.3 -0.2
# 7   0.0 -0.9  0.4  0.4 -1.5 -0.7  1.2 -1.0  0.5 -0.3  0.1  1.2
# 8  -0.2  0.4  0.8 -0.6 -0.5 -0.4  1.7  0.6  0.4 -1.5  1.3 -1.7
# 9   0.3 -0.8  0.3  1.0 -0.6 -1.0  1.1 -1.3  0.5 -0.1  1.2  1.9
# 10  0.4 -0.1 -0.6 -0.8  1.8 -0.1 -0.8 -0.7  0.8 -2.4 -0.7  0.5
 
fit <- lm(cbind(Y1, Y2, Y3, Y4, Y5, Y6, Y7, Y8, Y9) ~ X1 + X2 + X3, data = df)
fit_summary <- summary(fit)
 
fit_summary_t_values <- list()
for(i in 1:length(fit_summary)) {
  fit_summary_t_values[[i]] <- fit_summary[[i]]$coefficients[ , 3]
}
 
names(fit_summary_t_values) <- names(fit_summary)
 
fit_summary_t_values
# $`Response Y1`
# (Intercept)          X1          X2          X3 
#   0.6831313   0.8561820  -0.2167878   0.6841317 
# 
# $`Response Y2`
# (Intercept)          X1          X2          X3 
#  -3.5742329  -2.6511756   0.1942444  -3.4450485 
# 
# $`Response Y3`
# (Intercept)          X1          X2          X3 
#   0.2867515   0.4443562  -0.9089214  -0.0815937 
# 
# $`Response Y4`
# (Intercept)          X1          X2          X3 
#  1.24356131  0.97643032  0.08287713  0.32310187 
# 
# $`Response Y5`
# (Intercept)          X1          X2          X3 
#   0.2480316  -0.2911459  -1.5378596  -0.5451000 
# 
# $`Response Y6`
# (Intercept)          X1          X2          X3 
#  -1.8243273  -0.2313444  -1.0470637  -1.0220742 
# 
# $`Response Y7`
# (Intercept)          X1          X2          X3 
#   2.2683215   0.7558973   0.1398253  -1.2021584 
# 
# $`Response Y8`
# (Intercept)          X1          X2          X3 
#   0.2231671   1.5707622   0.5847195  -1.5914540 
# 
# $`Response Y9`
# (Intercept)          X1          X2          X3 
#   2.7181012  -0.5316540  -1.0781624  -0.2181151

I’m sure this code could be improved in terms of efficiency. However, it should provide you with the result you are looking for.

I hope that helps!

Joachim

Ludvig Ost
November 9, 2021 8:39 am

Thank you so much for helping me Joachim. The code worked perfectly.

Could you also show me how I calculate tracking error?

Regards,
Ludvig

Reply
- Joachim
  November 9, 2021 8:45 am
  
  That’s great to hear, glad it helped!
  
  I’m not an expert on calculating tracking errors. However, I found this function, which seems to be what you are looking for: https://rdrr.io/cran/PerformanceAnalytics/man/TrackingError.html
  
  Regards,
  Joachim
  
  Reply
SH
December 6, 2021 10:47 pm

Thanks for clarifying!
Will there be any ways to separately save the p-value from F-statistic category?

Reply
- Joachim
  December 7, 2021 6:47 am
  
  Thank you, glad it helped! Could you explain your question in some more detail?
  
  Regards,
  Joachim
  
  Reply
su
February 16, 2022 12:31 pm

Hi Joachim. I am very very bad at mathematics and statistics. I have recently done a simple regression and I got negative t values like the output mentioned here. Does that mean the model is bad? Is it common to have negative t values and if so what is the reason for that? Thank you

Reply
- Joachim
  February 16, 2022 2:26 pm
  
  Hey Su,
  
  Please have a look at this thread on Research Gate. It discusses your question.
  
  Regards,
  Joachim
  
  Reply