quantile Function in R (6 Examples)
This tutorial shows how to compute quantiles in the R programming language.
The article is mainly based on the quantile() R function. So let’s have a look at the basic R syntax and the definition of the quantile function first:
Basic R Syntax of quantile():
quantile(x)
Definition of quantile():
The quantile function computes the sample quantiles of a numeric input vector.
In the following R tutorial, I’ll explain in six examples how to use the quantile function to compute metrics such as quartiles, quintiles, deciles, or percentiles.
Let’s dive in!
Example 1: Basic Application of quantile() in R
In the first example, I’ll illustrate how to use the quantile function in its simplest way. Let’s create an exemplifying numeric vector first:
set.seed(15051) # Set seed for reproducibility x <- round(runif(1000, 0, 100)) # Create uniformly distributed data x # Print data to RStudio console # 73 44 4 2 3 78 15 38 59 70 80...
Our example vector contains 1,000 elements between the range of 1 and 100.
Now, we can apply the quantile R function to this vector as follows:
quantile(x) # Apply quantile function # 0% 25% 50% 75% 100% # 0 23 50 75 100
As you can see based on the RStudio console output, the quantile function returns the cutpoints (i.e. 0%, 25%, 50%, 75%, and 100%) as well as the corresponding quantiles.
Note: By default, the quantile function is returning the quartile (i.e. five cutpoints). Later on, I’ll show you how to get other metrics as well.
However, let’s first have a look at a common problem when the quantile function is applied…
Example 2: Handling NA Values with the quantile Function
In this example, you’ll learn how to deal with missing data (i.e. NA values) in the input vector. Let’s first insert an NA value to our example data:
x_NA <- c(x, NA) # Create example data with NA
Now, if we apply the quantile function to this vector, the quantile function returns an error message:
quantile(x_NA) # Apply quantile function to NA vector # Error in quantile.default(x_NA)
Fortunately, we can easily fix this error by specifying na.rm = TRUE within the quantile command:
quantile(x_NA, na.rm = TRUE) # Use na.rm argument # 0% 25% 50% 75% 100% # 0 23 50 75 100
Same output as in Example 1 – Perfect.
Example 3: Extract Quantile Values Only
AS you have seen based on the previous examples, the quantile function returns the cutpoints AND the corresponding values to the RStudio console. In some cases, however, we might prefer to keep only the quantile values.
In this case, we can simply apply the unname function to the output of the quantile function. Have a look at the following R code:
unname(quantile(x)) # Get only the quantile values # 0 23 50 75 100
Based on this R code, we only get the quantile values.
Example 4: Quantile by Group
In this example I’ll show you how to calculate the quantiles of certain subgroups. For the example, I’m going to use the Iris data matrix. Let’s load the data to R:
data(iris) # Load Iris data head(iris) # Head of Iris data

Table 1: The Iris Data Frame.
The Iris data set contains several numeric variables and the grouping variable Species.
We can now produce a data matrix of quantiles of the first column grouped by the Species column with the following R syntax:
do.call("rbind", tapply(iris$Sepal.Length, # Specify numeric column iris$Species, # Specify group variable quantile)) # 0% 25% 50% 75% 100% # setosa 4.3 4.800 5.0 5.2 5.8 # versicolor 4.9 5.600 5.9 6.3 7.0 # virginica 4.9 6.225 6.5 6.9 7.9
Note that it would also be possible to calculate quantiles by group based on functions of the tidyverse. This tutorial demonstrates how to calculate quantiles by group using the dplyr package.
Example 5: Quartiles, Quintiles, Deciles, Percentiles & Many More
As I told you before, the quantile function returns the quartile of the input vector by default. However, we can use the probs argument to get basically any quantile metric that we want.
With the following R codes, we can calculate the median…
quantile(x, probs = 0.5) # Median # 50% # 50
…tertiles…
quantile(x, probs = seq(0, 1, 1/3)) # Tertiles # 0% 33.33333% 66.66667% 100% # 0 34 68 100
…quartiles (as it would also be computed by default)…
quantile(x, probs = seq(0, 1, 1/4)) # Quartiles # 0% 25% 50% 75% 100% # 0 23 50 75 100
…quintiles…
quantile(x, probs = seq(0, 1, 1/5)) # Quintiles # 0% 20% 40% 60% 80% 100% # 0 18 40 61 80 100
…sextiles…
quantile(x, probs = seq(0, 1, 1/6)) # Sextiles # 0% 16.66667% 33.33333% 50% 66.66667% 83.33333% 100% # 0 15 34 50 68 83 100
…septiles…
quantile(x, probs = seq(0, 1, 1/7)) # Septiles # 0% 14.28571% 28.57143% 42.85714% 57.14286% 71.42857% 85.71429% 100% # 0 13 27 43 58 72 86 100
…octiles…
quantile(x, probs = seq(0, 1, 1/8)) # Octiles # 0% 12.5% 25% 37.5% 50% 62.5% 75% 87.5% 100% # 0.000 11.875 23.000 38.000 50.000 63.000 75.000 88.000 100.000
…deciles…
quantile(x, probs = seq(0, 1, 1/10)) # Deciles # 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% # 0 9 18 29 40 50 61 71 80 90 100
…duo-deciles…
quantile(x, probs = seq(0, 1, 1/12)) # Duo-deciles or dodeciles # 0% 8.333333% 16.66667% 25% 33.33333% 41.66667% 50% 58.33333% 66.66667% 75% 83.33333% 91.66667% 100% # 0 8 15 23 34 42 50 59 68 75 83 92 100
…hexadeciles…
quantile(x, probs = seq(0, 1, 1/16)) # Hexadeciles # 0% 6.25% 12.5% 18.75% 25% 31.25% 37.5% 43.75% 50% 56.25% 62.5% 68.75% 75% 81.25% 87.5% 93.75% 100% # 0.0000 7.0000 11.8750 17.0000 23.0000 30.1875 38.0000 44.0625 50.0000 57.0000 63.0000 70.0000 75.0000 81.0000 88.0000 94.0000 100.0000
…ventiles…
quantile(x, probs = seq(0, 1, 1/20)) # Ventiles, vigintiles, or demi-deciles # 0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50% 55% 60% 65% 70% 75% 80% 85% 90% 95% 100% # 0.00 5.00 9.00 13.00 18.00 23.00 29.00 36.00 40.00 45.55 50.00 56.00 61.00 66.00 71.00 75.00 80.00 85.00 90.00 95.00 100.00
…percentiles…
quantile(x, probs = seq(0, 1, 1/100)) # Percentiles # 0% 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 11% 12% 13% ... # 0.00 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 8.91 9.00 10.00 11.00 12.00 ...
…or permilles:
quantile(x, probs = seq(0, 1, 1/1000)) # Permilles or milliles # 0.0% 0.1% 0.2% 0.3% 0.4% 0.5% 0.6% 0.7% 0.8% 0.9% 1.0% 1.1% 1.2% 1.3% ... # 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.993 1.000 1.000 1.000 1.000 1.000 1.987 ...
Example 6: How to Visualize Quantiles
Quantiles are often used for data visualization, most of the time in so called Quantile-Quantile plots.
Quantile-Quantile plots can be created in R based on the qqplot function. Let’s do this in practice!
First, we need to create a second vector:
y <- x + rnorm(1000, 0, 30) # Create y-data
Now, we can print a qqplot of our two example vectors with the qqplot function as follows:
qqplot(x, y) # Quantile-Quantile plot of x & y
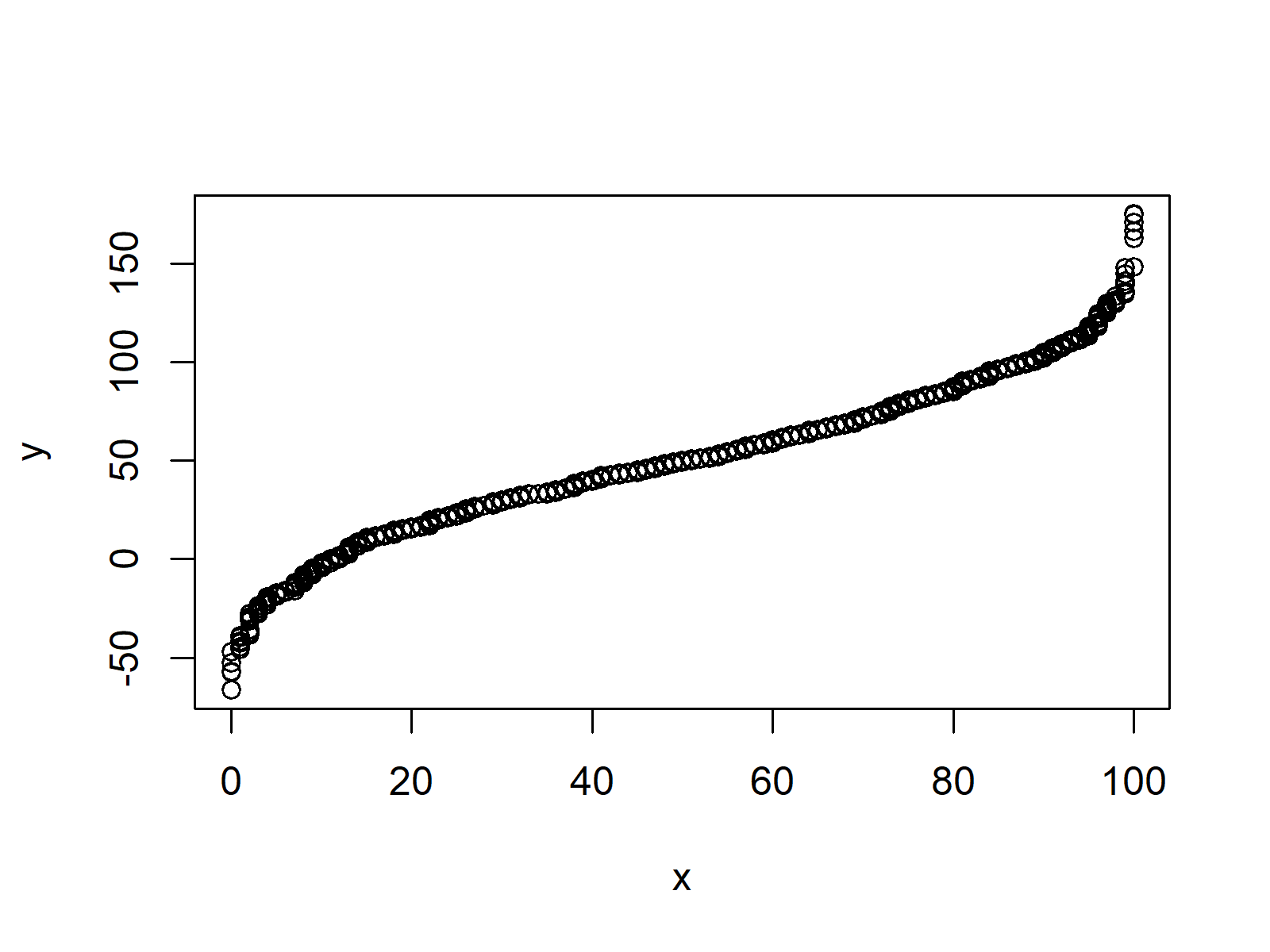
Figure 1: Basic Quantile-Quantile Plot in R.
Video, Further Resources & Summary
Below, you can find a video on the Statistics Globe YouTube channel where I describe the steps of this tutorial in expanded detail:
Quantiles can be a very useful weapon in statistical research. A topic we haven’t talked about yet is the commonly used quantile regression. If you want to learn more about quantile regressions, you can have a look at the following YouTube video of Anders Munk-Nielsen:
Furthermore, you may have a look at the other R tutorials on Statistics Globe:
- Quantile-Quantile Plot in R
- Compute Interquartile Range (IQR) in R
- The Empirical Cumulative Distribution Function (ecdf R Function)
- The do.call R Function
- R Functions List (+ Examples)
- The R Programming Language
At this point, I hope you know how to deal with the quantile function in the R programming language. However, if you have any questions don’t hesitate to let me know in the comments section below.







17 Comments. Leave new
do.call(“rbind”,
tapply(iris$Sepal.Length, # Specify numeric column
iris$Species, # Specify group variable
quantile))
in this scrip how to set the row.names or how to know which row belongs to which category?
Hi Kumar,
Thank you for your question. Could you elaborate your question in some more detail? I’m not sure if I understand the question correctly.
Regards,
Joachim
Hi, Thanks for the post! I was wondering how would you do if you want a first group which contained between 0-5% and then separate in tertiles (5-100%).
Hey Chris,
Thanks for the comment! If I understand your question correctly, then this is what is shown in Example 5 – ventiles. Does this solve your problem?
Regards,
Joachim
Hi Joachim, thank you for your post. It’s very useful, but i have some questions about type argument which you haven’t mention in your post.
# method for default
quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE,
names = TRUE, type = 7, …)
type
an integer between 1 and 9 selecting one of the nine quantile algorithms detailed below to be used.
i have just some informations, but i can’t understand it very well. Could you please explain to me if you know about the usage of this argument ? Thanks in advance.
Hey Solène,
First of all, thank you for the kind words! Glad you like the article!
Regarding your question: The type argument allows you to specify different algorithms for the computation of the quantiles. The different types and formulas are described in the help documentation of the quantile function.
You may open the help documentation using the code ?quantile, and then you will find a detailed description of the algorithms under the section “Type”.
Regards,
Joachim
I am looking at the variable ‘thorax’ from the data ‘fruitflies’ in the faraway package. I ran the R function ‘quantile’ on ‘thorax.
> data(fruitfly)
> dim(fruitfly)
[1] 124 3
> head(fruitfly)
thorax longevity activity
1 0.68 37 many
2 0.68 49 many
3 0.72 46 many
4 0.72 63 many
5 0.76 39 many
6 0.76 46 many
> Deciles Deciles
10% 20% 30% 40% 50% 60% 70% 80% 90%
0.72 0.76 0.80 0.82 0.84 0.84 0.88 0.88 0.92
Identify all the four quintiles:
I quintile =
II quintile =
III quintile =
IV quintile =
Can you explain this and let me know the answer. I am a beginner. please help me with this.
Hey Nandini,
Quintiles can be calculated as shown in the following code:
You would have to replace x by the data you want to calculate the quintiles for.
Regards,
Joachim
Hi, This is super helpful. I have been trying to obtain 98th percentile from a data frame with grouping. This basically combines example 4 with the first example of 5. I tried this:
do.call(“rbind”,
tapply(MT_2.5_2001$Arithmetic.Mean,
MT_2.5_2001$County.Name,
quantile( probs=0.98))
**No default data, so then tried this:
do.call(“rbind”,
tapply(MT_2.5_2001$Arithmetic.Mean,
MT_2.5_2001$County.Name,
quantile(MT_2.5_2001$Arithmetic.Mean, probs=0.98)))
With this error code: Error in match.fun(FUN) :
‘quantile(MT_2.5_2001$Arithmetic.Mean, probs = 0.98)’ is not a function, character or symbol
do.call(“rbind”,
tapply(MT_2.5_2001$Arithmetic.Mean,
MT_2.5_2001$County.Name,
quantile(MT_2.5_2001$Arithmetic.Mean, probs=0.98)))
error in match.fun(FUN) :
‘quantile(MT_2.5_2001$Arithmetic.Mean, probs = 0.98)’ is not a function, character or symbol
and tried using dplyr, which spits out one number, not grouped data
MT_2.5_2017.98%
group_by(County.Name) %>%
summarize(quant98 = ~quantile(Arithmetic.Mean, probs= 0.98))
MT_2.5_2017.98
Any suggestions?
Hi Bethany,
Thank you so much for the kind words, glad you find my tutorials helpful!
I apologize for the delayed reply. I was on a long vacation, so unfortunately I wasn’t able to get back to you earlier. Do you still need help with your syntax?
Regards,
Joachim
Hi Joachim, No problem. I either figured it out or found a work around. I am an R novice so doing a lot of learning by internet blogs like yours. Thank you!
Hi Bethany,
It’s great to hear that you found a solution, and thanks a lot for the very kind words regarding my blog! 🙂
Regards,
Joachim
Hi,
0
I have a continuous variable in my dataset with such a distribution:
summary(emissions$NMVOC_gram)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0 256 547 15802 1074 50818630
how can i categorize this variable to unequal levels of extremely high to extremely low, low, high, and medium in R or excel?
thank you for the help
I tried the cut function in r but the result was not what I expected, actually, I do not know how I should define the breaks, in my data the 3rd Qu. is lower than the Mean.
Hi Samin,
Sorry for the late response. Could you find a solution? Here is what I found by a small search. You can split your values into quantiles via the split_quantiles() function of the fabricatr package. Then you can rename your values. See below:
Regards,
Cansu
thank you very much for your help,
how to get a particular quantile value like q1 or q3? help is much appreciated.
Hello Rokesh,
You can use the same code setting shown in the tutorial as follows:
Regards,
Cansu