Introduction to Hypothesis Testing | Theoretical Concepts & Example

 

Hypothesis testing is everywhere in data analysis. Every time you see a p-value or hear about statistical significance, they relate to a hypothesis test. But have you wondered why you need to perform hypothesis testing? After all, you have your data and can view the summary results. Why do more?

Furthermore, what’s behind the procedure of comparing your p-values to your significance level to determine statistical significance? And, what does statistical significance mean anyway?

In this introduction to hypothesis testing, I pull back the curtain and answer all these questions. I’ll explain the larger picture of why you need to use these tests, clarify the details behind the procedure, and explain what it all means. I’ll even throw in a little bit about confidence intervals and work through an example at the end!

Table of contents:

Note: This article was written by Jim Frost – founder of statisticsbyjim.com and author of statistical books such as “Introduction to Statistics: An Intuitive Guide” and “Hypothesis Testing: An Intuitive Guide”. Please find more information about Jim at the end of this page!

 

Hypothesis Testing and Inferential Statistics

Hypothesis testing is a vital part of inferential statistics. That’s the branch of statistics where you use random samples to draw inferences about entire populations. For example, you might use a sample mean to estimate the population mean. Or perhaps you want to evaluate differences between groups in a population or need to establish that a relationship between variables exists at the population level.

Inferential statistics is crucial because, for most studies, you don’t want to apply the results only to the relatively few people or items in your sample. Instead, you want to generalize the results to a broader population.

Imagine you’re a scientist experimenting with a new medication. Your experimental design has a treatment and control group. If the health outcome for the treatment group is better than the control group, your medicine has a positive effect. However, knowing that the drug helps only those few people in your sample does very little good for either science or the rest of society. You want to be able to apply those results to the entire population.

That’s where inferential statistics and hypothesis testing enter the picture.

I’ll use this medicine example throughout this article, but the same ideas apply to whatever you’re studying.

 

Hypothesis Testing Addresses a Major Drawback of Samples

You gain tremendous benefits by working with a random sample. In most cases, it is simply not logistically possible or financially feasible to observe an entire population. The only alternative is to assess a sample.

Despite their ubiquity in studies, samples have a significant downside—sampling error.

Sampling error is the difference between your sample statistic and the actual population value, which statisticians call a population parameter. Suppose you’re using a sample mean to estimate the population mean. Thanks to sampling error, your sample mean is virtually guaranteed not to equal the population mean exactly.

Taking this idea further, any effect you observe in a sample might be sampling error rather than an actual effect or relationship in the population. If sampling error caused the apparent effect, the next time someone performs the same study, the results might differ.

Let’s apply this issue to our medicine experiment. In our sample, we observe that the treatment group has better health outcomes than the control group. However, that sample difference does not equal the population difference. Even though we see an effect in our sample, there may be no effect in the population. In that scenario, the difference in our sample is an artifact caused by sampling error.

If that’s the case and the medication goes to market, the public won’t obtain the benefits you expect from the sample statistics. That can be a costly mistake!

Hypothesis tests help you draw the correct inferences from your sample by helping you distinguish between sampling error and real effects.

That’s why you need to perform hypothesis testing.

 

Basic Concepts of Hypothesis Tests

It is important to understand some basic concepts when applying hypothesis tests. In the following sections, I’ll cover some of these basic concepts to help you understand the procedure.

 

Hypothesis Tests

Hypothesis tests use sample data to evaluate two mutually exclusive statements about the characteristics of a population. Analysts refer to these statements as the null hypothesis and alternative hypotheses. The hypothesis test appraises your sample data in conjunction with an estimate of the sampling error. Ultimately, the test determines whether the data favor the null or alternative hypothesis.

 

Effects

Effects represent the relationships between variables and differences between groups in a population. No effect indicates there is no difference between groups or no correlation between variables. Conversely, when an effect exists, a difference between groups or a correlation between variables exists in the population.

For example, in our fictitious medicine study, the mean difference between the treatment and control groups is the effect. Other examples of effects include the relationship between marketing and sales, the proportion of successful outcomes in a new versus old educational program, and whether a change in banking procedures affects transaction time.

You never know the size of the actual population effect. However, hypothesis tests use your sample data to help determine whether a population effect exists and estimate its size.

 

Null Hypothesis

The null hypothesis is one of the mutually exclusive statements about the population. Usually, it states that the effect size equals zero. In other words, it says an effect does not exist in the population.

In all hypothesis tests, the analysts are assessing some type of effect. There is a relationship that the analysts want to ascertain. Unfortunately, the effect that they’re hoping to find might not exist. Such is the life of a researcher! Statisticians refer to this non-effect as the null hypothesis.

For example, in our medicine study, the null hypothesis states that the difference between the treatment and control group equals zero. The medicine does not affect the health outcome.

For most hypothesis tests, analysts want to reject the null hypothesis, indicating that the effect likely exists in the population rather than just being a sampling error artifact.

The null hypothesis is the default theory that requires strong evidence to reject before you can get excited over promising new findings!

 

Alternative Hypothesis

The alternative hypothesis is the other statement about the characteristics of the population. Typically, it states that an effect does not equal zero, suggesting that it exists in the population.

When your sample contains sufficient evidence, you can reject the null hypothesis and favor the alternative.

In our medicine study, the alternative hypothesis states that the difference between the treatment and control group does not equal zero. The medicine affects the health outcome.

 

P-values

In simple terms, p-values indicate how inconsistent your sample data are with the null hypothesis. Lower values indicate stronger evidence against the null hypothesis.

In more technical terms, p-values are the probability of obtaining the sample effect you observed, or larger, if the null hypothesis is correct.

P-values are notoriously easy to misinterpret when you try to interpret the value itself using the technical definition. Unfortunately, p-values incorporate complicated math, nuanced theory, and convoluted probability issues that work together to promote misunderstandings. That’s too much to cover in this overview!

Consequently, I’ll stick with the simpler definition that p-values represent the strength of your sample evidence against the null hypothesis. For more information about this topic, read my post about Interpreting P-values.

 

Significance Levels

Significance levels are an evidentiary standard. Ideally, analysts set this standard before conducting the study. Significance levels indicate how strongly the sample data must contradict the null hypothesis before rejecting it for the entire population. The significance level is also known as alpha or α.

This measure is defined by the likelihood of rejecting a true null hypothesis. Think of it as the chance of saying that an effect exists when it does not exist—the probability of a false positive.

For example, the standard significance level is 0.05, which represents a false-positive risk of 5%.

 

The Hypothesis Testing Decision Rule and Statistical Significance

The decision rule for hypothesis testing procedures involves comparing your p-value to the significance level. Here’s why you need to do that.

The p-value represents the strength of the evidence in your sample against the null hypothesis. The significance level indicates how strong the evidence must be before rejecting the null. Consequently, by comparing the p-value to the significance level, you’re determining whether the strength of the evidence exceeds the threshold to declare statistical significance.

Compare your p-value to the significance level to determine the following:

• When your p-value is less than or equal to the significance level, reject the null hypothesis. Your results are statistically significant. Mnemonic aid: If the p-value is low, the null must go!
• When your p-value is greater than the significance level, you fail to reject the null hypothesis. Your results are not statistically significant.

Let me elaborate a bit on the above conditions.

When your results are statistically significant, your sample evidence is strong enough to favor the hypothesis that the effect exists in the population. Remember, it’s all about using samples to draw conclusions about a population.

On the other hand, when you fail to reject the null, you obviously cannot conclude that the effect exists in the population. However, your results do not prove there is no population effect. There is a reason for the weird phrasing, “fail to reject the null.” It has to do with the idea that you can’t prove a negative. For more information, read my article about Failing to Reject the Null Hypothesis.

 

Example Hypothesis Test for the Medication Study

Finally, let’s use a two-sample t-test to evaluate our hypothetical medicine experiment. You can download the dataset to try it yourself: MedicineExperiment.

For our study, the 2-sample t-test has the following hypotheses:

• Null hypothesis: The population means for the treatment and control groups are equal.
• Alternative hypothesis: The population means for the two groups are not equal.

 

 

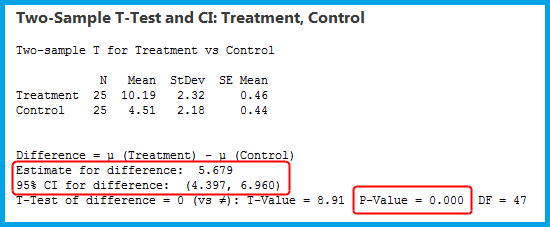
Because our p-value (0.000) is less than the standard significance level of 0.05, we can reject the null hypothesis. Our sample data support the claim that the population means are different. Specifically, the Treatment Group’s mean is greater than the Control Group’s mean. We have enough evidence to infer that this effect exists in the population and not just our sample.

The sample estimate of the mean difference, or effect, is 5.679. However, that estimate is based on 50 observations split between the two groups, and it is unlikely to equal the population difference. Remember, sampling error introduces a margin of error around all estimates. You can use the confidence interval (CI) of the difference to account for that margin of error and determine a range that likely contains the population effect.

The CI estimates that the mean difference between the two groups for the entire population is likely between 4.397 and 6.960. Because the confidence interval excludes zero (no difference between groups), we can conclude that the population means are different. Use CIs to help you understand the precision of the estimate and determine the real-world importance of your findings.

After reading this article, I hope you understand the need for performing hypothesis tests, the basic concepts, why we compare p-values to the significance level, what statistical significance means, and how confidence intervals fit in!

 

Further Resources

So far, we have covered some of the most important theoretical aspects of hypothesis testing. In case you want to apply the methods shown in this tutorial in practice, you may have a look at the following video exercise. In the video, Andre Hingston explains how to perform a hypothesis test using the R programming language.

 

 

Furthermore, you may have a look at some of the related tutorials on Statistics Globe:

• Calculate Descriptive Statistics in R
• Calculate Linear Regression Model & Extract Standard Error, t-Value & p-Value
• How to Write a Model Formula with Many Variables in R
• Introduction to the R Programming Language

In summary: In this tutorial, Jim Frost has explained how to apply statistical hypothesis test. You have learned some of the most important theoretical concepts, and you have learned how to apply hypothesis test in practice. In case you are interested in more tutorials about similar topics, you may have a look at Jim’s other content.