Confirmatory Factor Analysis (CFA) | Meaning & Interpretation

In this tutorial, I’ll introduce Confirmatory Factor Analysis (CFA), which is a multivariate statistical technique researchers use to to confirm hypotheses or theories about the underlying structures of certain datasets.

The table of content is structured as follows:

Let’s dive into it!

Introduction

Confirmatory Factor Analysis (CFA) is a statistical technique used primarily in the social sciences. CFA allows researchers to validate their proposed measurement models by testing how well the *observed variables (e.g., questionnaire items) represent the underlying *factors (latent variables) they are theorized to measure. Unlike exploratory factor analysis (EFA), which seeks to identify potential underlying factor structures, CFA tests whether a particular structure fits the data.

Instead of “discovering” or exploring potential relationships between variables, as in exploratory factor analysis, CFA is designed to test a predefined model based on theoretical expectations. Relatedly, in CFA, the starting point should be a theory or empirical findings, which could come from existing literature, previous EFA results, or well-established theoretical models.

Like other statistical techniques, CFA operates under certain assumptions. It’s essential to verify these assumptions, as violating them can lead to biased, misleading, or incorrect results. Let’s elaborate on them!

Assumptions

Linearity: The relationships between observed variables and the underlying unobserved latent variables are assumed to be linear. In the typical CFA, observed variables are defined as linear functions of the latent variables. An observed variable x is formalized as x = λξ + δx, where λ refers to factor loadings, ξ refers to underlying factors and δx refers to measurement error of x.

Multivariate Normality: The observed variables should ideally follow a multivariate normal distribution. This means that all combinations of variables are jointly normally distributed. This assumption can significantly impact some fit indices and standard errors. In such a case, robust estimation techniques could be performed to avoid the effect of normality violation.

Sample Size Adequacy: An adequate sample size is crucial for stable factor solutions. A common recommendation is a ratio of at least 5 participants per variable, but larger samples are generally better.

Over identification: The model should be over-identified. This means there should be more observed variances and covariances than parameters estimated (estimated variances, covariances and factor loadings). One common way is to ensure that one of the factor loadings is fixed to value 1. By doing so, the scale of the latent variable will also be defined. For further details, see page 80 in Confirmatory Factor Analysis for Applied Research (Brown, 2006).

If your data meets these assumptions and you intend to test your measurement model, then you can perform CFA. Let’s see the steps of CFA!

Steps to Perform CFA

In this section, the steps of performing CFA are theoretically explained. For the practical implementation in R, see Confirmatory Factor Analysis in R to be published soon.

Model Specification

Based on theory or previous analyses, the practitioner should decide which observed variables are connected to which latent variables, in other words, which observed variables will load onto which latent variables.

Imagine, based on prior empirical research, you hypothesized that an individual’s general well-being can be measured by two latent factors: physical health and emotional health.

To measure these constructs, you prepared a questionnaire. In your measurement model, the first three questions measure physical health with the following:

• Q1: I feel physically active and energetic.
• Q2: I rarely get sick.
• Q3: I am satisfied with my overall physical health.

The next three questions measure emotional health with the following:

• Q4: I feel emotionally stable.
• Q5: I generally feel happy and contented.
• Q6: I rarely feel overwhelmed or anxious.

When you have a designed measurement structure, the next step will be gathering the related data.

Data Collection & Exploration

The data measuring the observed variables should be collected, cleaned and preprocessed before the analysis.

Parameter Estimation

In CFA, the process of parameter estimation revolves around determining the optimal values for factor loadings, factor covariances, and measurement error variances. The ultimate goal is to ensure that the covariance matrix predicted using these estimated parameters closely mirrors the observed covariance matrix from the data. Let’s take a look at the **estimations output regarding the well-being example.

 
Traditionally, Maximum Likelihood (ML) estimation method is employed when there is not enough evidence that the assumptions, like normality and sample size adequacy, are not violated. Otherwise, other robust techniques like WLSMV and MLR are performed.

The chosen estimation method uses an optimization algorithm, which iteratively adjusts parameter values to find the best-fitting parameters. Once the model converges, the software of choice (e.g., SPSS, R, Mplus) provides estimates for all parameters (as shown above), along with some fit statistics. Let’s take a closer look at these fit statistics next!

Fit Evaluation

It’s crucial to evaluate the fit of the model to ensure it adequately represents the data. Several fit indices can be used, each with its strengths and limitations. Here are some of the common fit indices:

Standardized Root Mean Square Residual (SRMR): This is the average difference between the observed correlation matrix (which represents the perfect prediction) and the matrix predicted by the model. Values less than 0.08 are generally considered indicative of a good fit.

Root Mean Square Error of Approximation (RMSEA): This adjusted chi-square statistic evaluates model fit in relation to the perfect model, penalizing model complexity. Values less than 0.05 indicate a close fit, values between 0.05 and 0.08 indicate a reasonable fit, and values greater than 0.10 may suggest a poor model fit.

Comparative Fit Index (CFI) and Tucker-Lewis Index (TLI): Both these indices compare the fit of the specified model to the null model. Values close to 0.95 or above are generally considered indicative of a good fit. The primary distinction between CFI and TLI is that TLI penalizes model complexity, whereas CFI does not.

It’s advisable to present and evaluate various fit indicators because each one offers its own advantages and drawbacks. For formulae, see this article.

Now, let’s take a look at the next step!

Model Respecification

If the fit indices indicate that the initial model does not fit the data well, then the hypothesized factor structure can be modified to achieve a better fit as long as the changes make theoretical sense or are based on substantive reasons.

The modification indices (MIs) and expected parameter change (EPC) are the statistics to consider in this step. They provide suggestions about which parameters to unconstrain (conventionally, the cross-loadings and error covariances are constrained to be zero in CFA).

MIs show how much the chi-square statistic would decrease if a fixed parameter was freely estimated. EPC shows the expected change in the magnitude of the parameter if a fixed parameter was unconstrained.

After making the modifications, the fit should be reassessed by a chi-square difference test or other comparing indices like AIC and BIC. Once the final structure is determined, the result can be interpreted and communicated visually.

Let’s see what kind of visual can be used!

Visualisation

The most common way to visualize CFA models is through path or factor diagrams. These diagrams consist of observed variables, latent factors, arrows indicating relationships, and error terms. You can see how the estimated covariance components are visualized below.

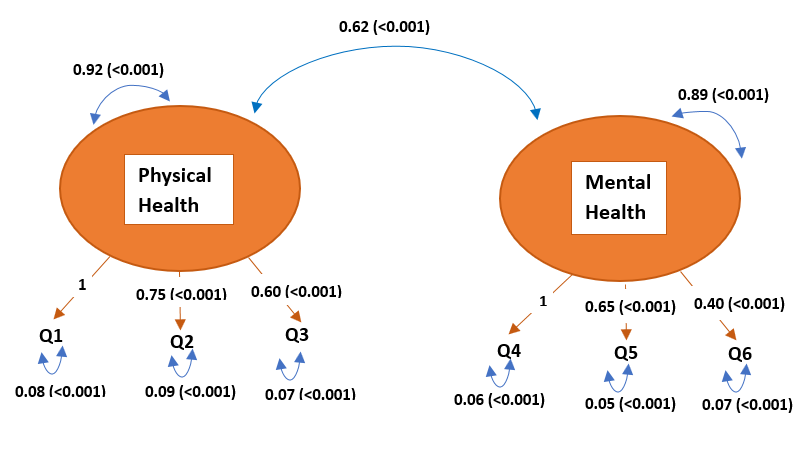
In the diagram above, the covariances are represented by the double-headed blue arrows indicating the direction of the relation. For instance, the arrowheads pointing to the same component represent the component’s covariance with itself, which is also known as its variance.

The orange arrows refer to the factor loadings. They point to the observed variables (Q1, Q2, etc.) since the latent variables cause/influence the observed variables contexually. The relation can described for Q2 as Q2 = Physical Health * 0.75 + e2, where e2 represents the associated measurement error with variance 0.09.

Please be aware that the blue arrows pointing to the observed variables (Q1, Q2, etc.) indicate the measurement error variance, not the observed variable variance. However, the measurement error variance is a part of the estimated observed variable variance, which can be written for Q2 as Var(Q2) = 0.75² * [Var(Physical Health) = 0.92] + [Var(e2)= 0.09].

*Observed variables can also be referred to as manifest variables, indicators, or endogenous variables, whereas latent variables can be referred to as factors, constructs, unobserved/underlying variables, or exogenous variables in the context of CFA.

**The example data is randomly generated; hence does not reflect any real analysis output.

Video, Further Resources & Summary

Do you need more explanations on how to perform CFA? Then, you might check out the following video of the Statistics Globe YouTube channel.

In the video tutorial, we explain how to conduct CFA to validate the proposed measurement model.

The YouTube video will be added soon.

Furthermore, you could have a look at some of the other tutorials on Statistics Globe:

• Intoduction to Factor Analysis
• Exploratory Factor Analysis (EFA)

This article has demonstrated steps of performing CFA. If you have further questions, you may leave a comment below.

This page was created in collaboration with Cansu Kebabci. You might have a look at Cansu’s author page to get more information about academic background and the other articles she has written for Statistics Globe.