Variance in R (3 Examples) | Apply var Function with R Studio

This tutorial shows how to compute a variance in the R programming language.

The article is mainly based on the var() function. The basic R syntax and the definition of var are illustrated below:

Basic R Syntax of var:

var(x)

Definition of var:

The var R function computes the sample variance of a numeric input vector.

In the following article, I’ll show in three examples how to use the var function in R.

So let’s move on to the examples!

Example 1: Compute Variance in R

In the examples of this tutorial, I’m going to use the following numeric vector:

x <- c(2, 7, 7, 4, 5, 1, 3)    # Create example vector

The computation of the variance of this vector is quite simple. We just need to apply the var R function as follows:

var(x)                         # Apply var function in R
# 5.47619

Based on the RStudio console output you can see that the variance of our example vector is 5.47619.

Note: The var function is computing the sample variance, not the population variance. How to calculate the population variance is what I’m going to show you next…

Example 2: Sample Variance vs. Population Variance

Before I show you how to compute a population variance, let’s quickly have a look at the difference between the two variances:

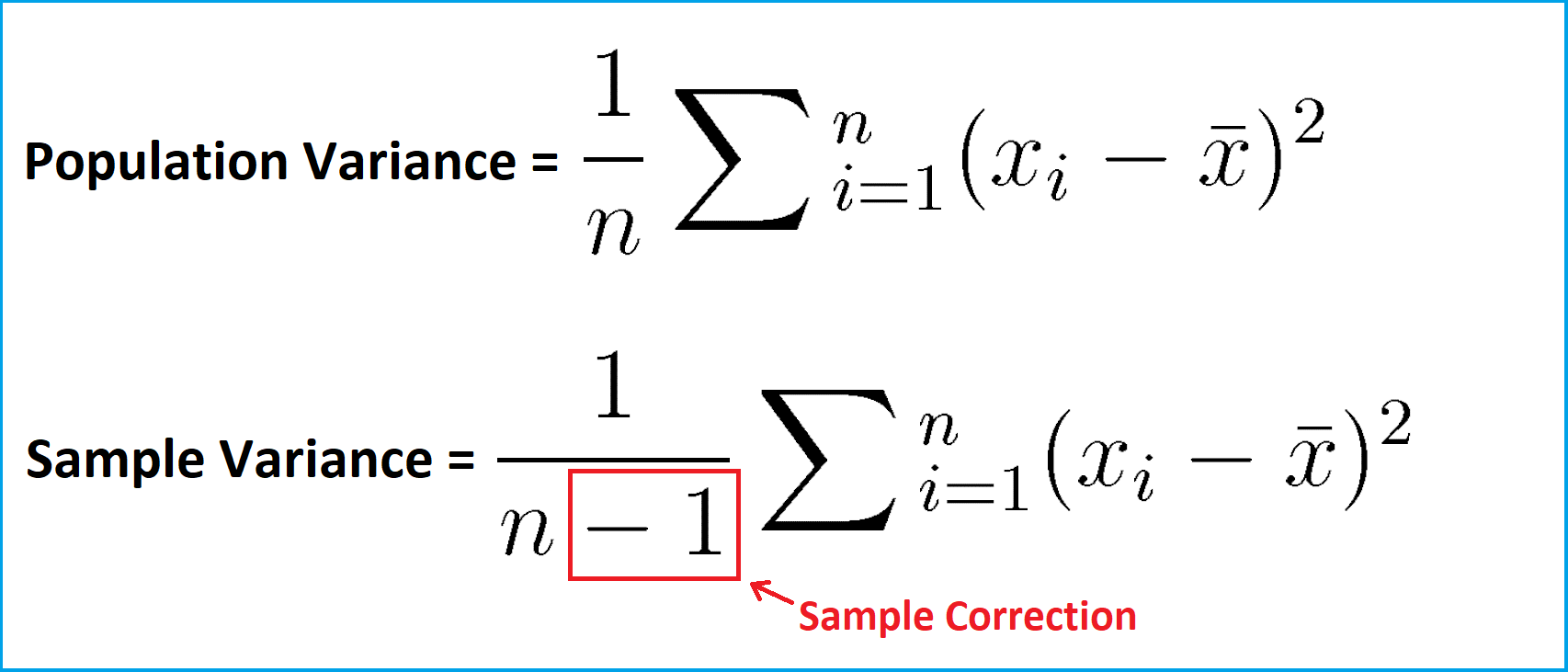
Figure 1: Comparison of Sample Variance and Population Variance.

The difference between sample and population variance is the correction of – 1 (marked in red). This correction does not really matter for large sample sizes. However, in case of small sample sizes there is large.

Let’s see how this looks in practice!

In R, we can create our own function for the computation of the population variance as follows:

var_pop <- function(x) {       # Create function for population variance
  mean((x - mean(x))^2)
}

Now, we can apply this function to our example data:

var_pop(x)                     # Apply population variance function
# 4.693878

The population variance of our example data is much smaller compared to the sample variance (population variance = 4.693878 vs. sample variance = 5.47619). It is therefore very important to use the correct variance function, especially when your sample size is small!

Example 3: Convert Variance to Standard Deviation

In scientific studies, the standard deviation is often preferred to the variance (standard deviation is easier to interpret).

Fortunately, the conversion from variance to standard deviation is easy. We simply need to compute the square root of our variance with the sqrt function:

sqrt(var(x))                   # Convert variance to standard deviation
# 2.340126

Alternatively, we can also calculate the standard deviation directly:

sd(x)                          # Compare with sd function
# 2.340126

Video, Further Resources & Summary

If you still have questions concerning the method I used in this tutorial, feel free to watch the video on my YouTube channel, where I describe the syntax more detailed:

In R, the variance can be computed quite easily. However, if you want to learn more about the concept of variances, I can recommend the following YouTube video of the MathAndScience channel:

Also, you might be interested in some of the other R tutorials of my website:

• Standard Deviation in R
• Standard Error in R
• R Functions List (+ Examples)
• The R Programming Language

In conclusion: this tutorial explained how to use the var command to compute the variance of numeric data in R. If you have any comments or questions, please let me know in the comments.