R Error in solve.default() : Lapack routine dgesv: system is exactly singular
In this post you’ll learn how to handle the “Error in solve.default() : Lapack routine dgesv: system is exactly singular” in the R programming language.
The article consists of two examples for the handling of errors. To be more precise, the page is structured as follows:
Let’s just jump right in!
Example 1: Reproduce the Error in solve.default() : Lapack routine dgesv: system is exactly singular
In Example 1, I’ll show how to replicate the error message in “solve.default() : Lapack routine dgesv: system is exactly singular”.
First, we have to create an example matrix in R:
my_mat1 <- matrix(1, ncol = 2, nrow = 2) # Create example matrix my_mat1 # Print example matrix
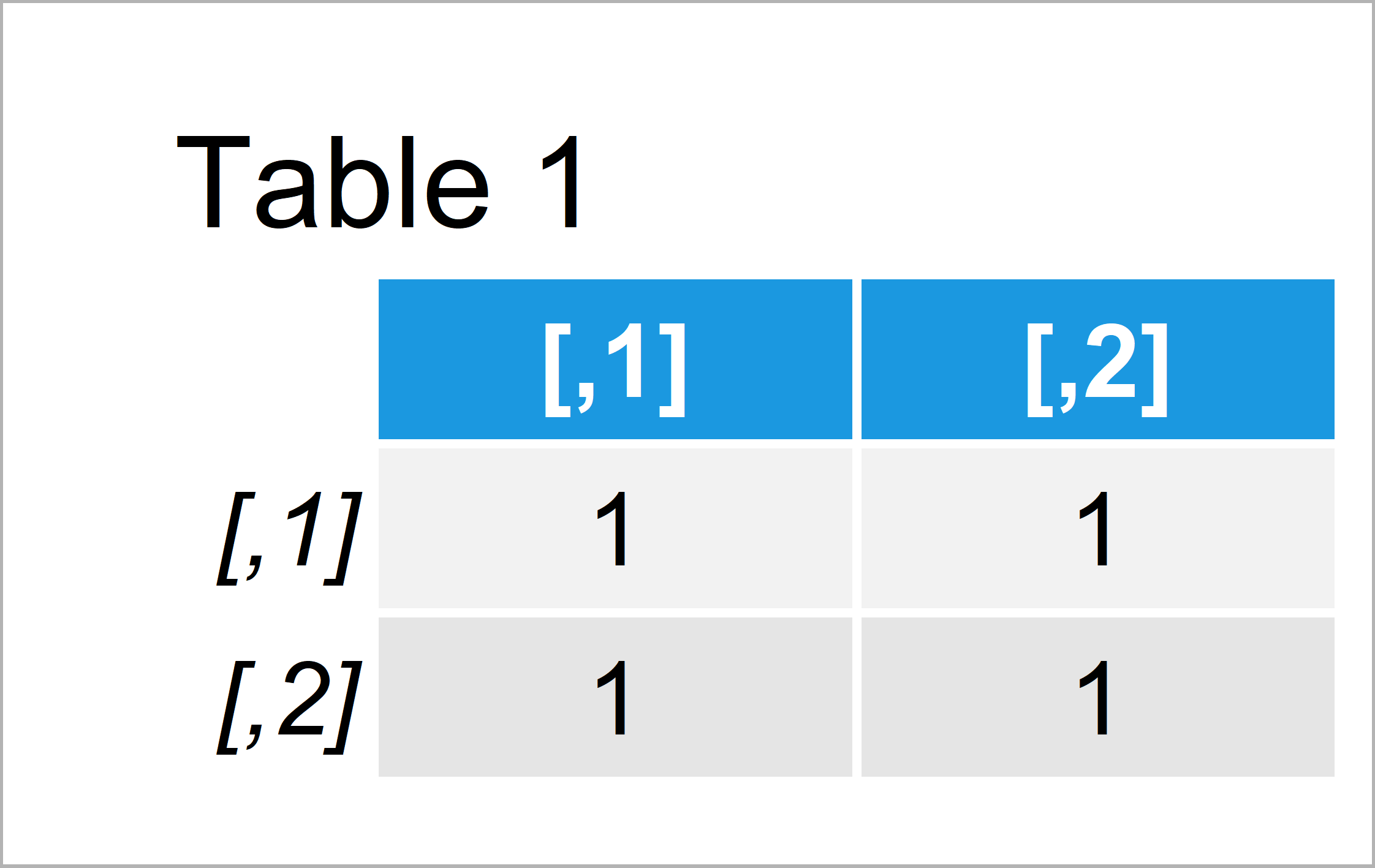
By running the previous R programming syntax we have constructed Table 1, i.e. a matrix containing only the value 0.
Let’s try to apply the solve function to this matrix:
my_mat1_solve <- solve(my_mat1) # Try to solve matrix # Error in solve.default(my_mat1) : # Lapack routine dgesv: system is exactly singular: U[2,2] = 0
As you can see, the previous R code has returned the “Error in solve.default() : Lapack routine dgesv: system is exactly singular”.
The reason for this is that we have tried to solve a system of equations that consists exactly of the same values. This is not possible and for that reason the R programming language returns the error message.
Note that this error can also occur when you have different values in your matrix. However, the error message typically tells that something is wrong with the input matrix.
Typical reason are that a matrix is singular and cannot be inverted or that some vectors are collinear.
So how can we fix this problem? That’s what I’ll explain next!
Example 2: Fix the Error in solve.default() : Lapack routine dgesv: system is exactly singular
This example shows how to properly apply the solve function to a matrix in R.
For this, we first have to create another matrix:
my_mat2 <- matrix(1:4, ncol = 2, nrow = 2) # Matrix with different values my_mat2 # Print second matrix
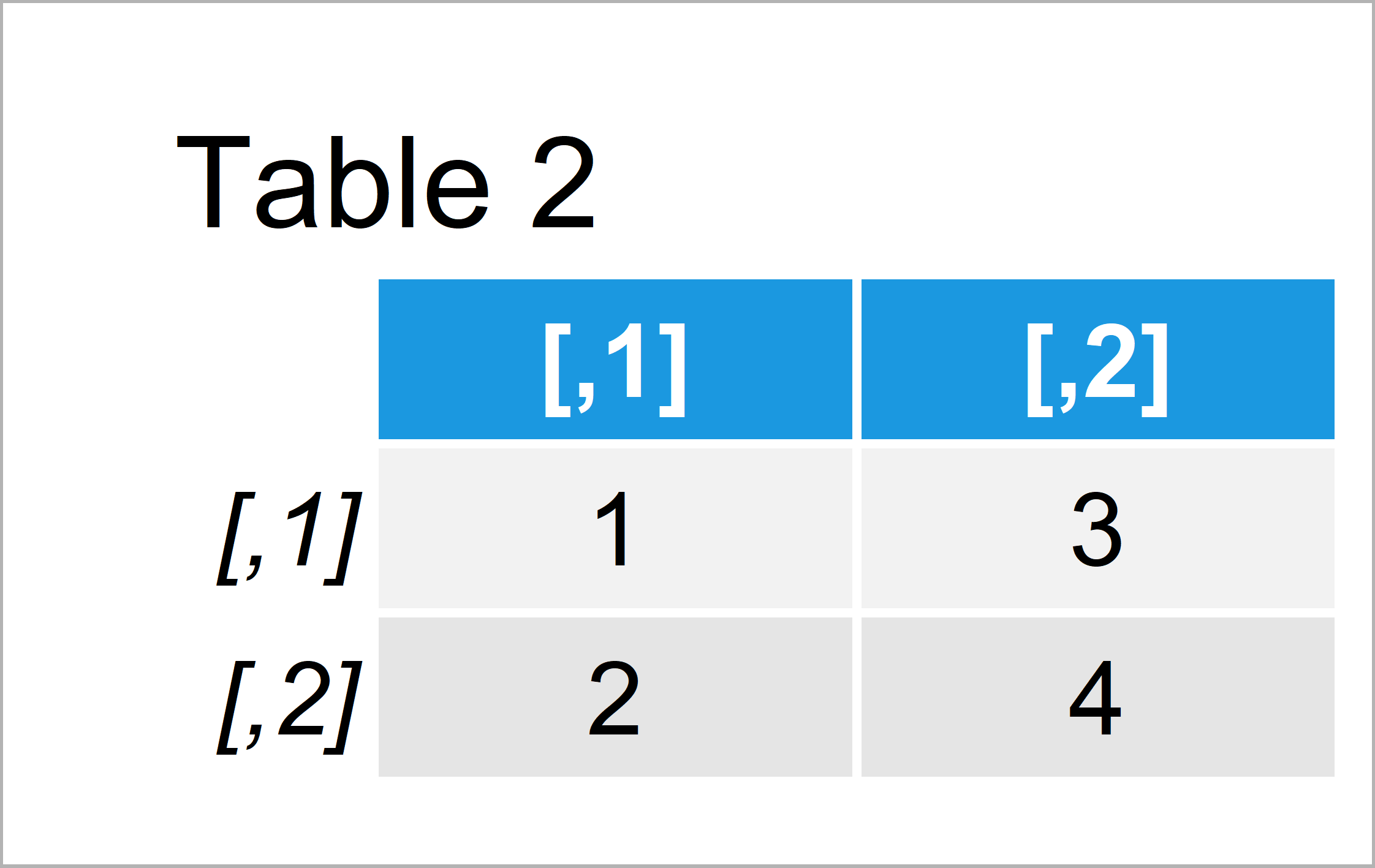
By running the previously shown R programming syntax we have constructed Table 2, i.e. a matrix that consists of different values.
Let’s apply the solve function to our new matrix:
my_mat2_solve <- solve(my_mat2) # Solve matrix my_mat2_solve # Print solved matrix
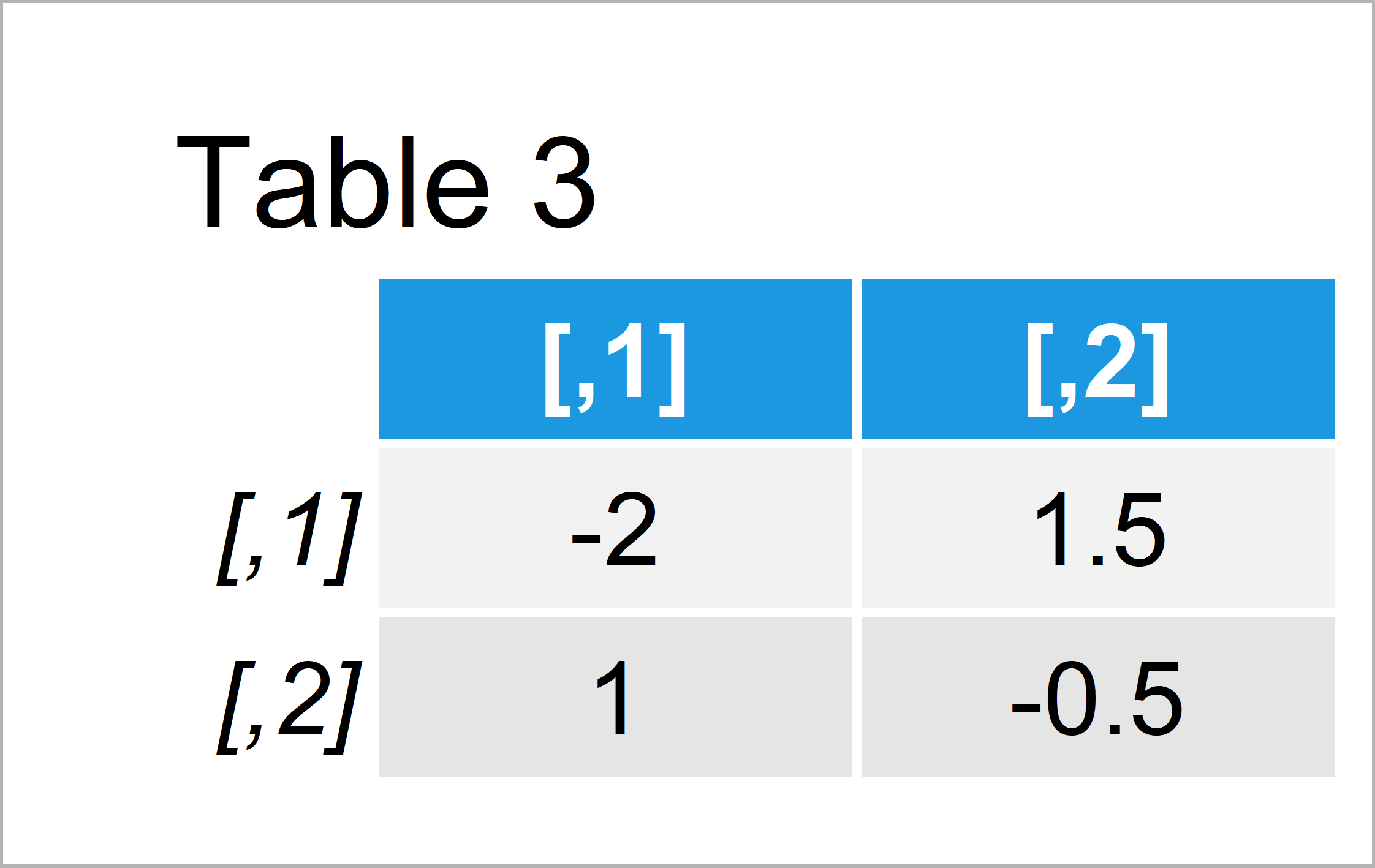
After running the previous syntax the matrix revealed in Table 3 has been created. As you can see, the application of the solve function worked fine.
Video & Further Resources
If you need further information on the R code of this tutorial, you may want to watch the following video of my YouTube channel. I show the examples of the present page in the video:
In addition, you might have a look at the other articles of this homepage. You can find a selection of tutorials below.
This tutorial has shown how to avoid the “Error in solve.default() : Lapack routine dgesv: system is exactly singular” in the R programming language. In case you have additional questions, let me know in the comments.







10 Comments. Leave new
I am trying to estimate the FEVD for VAR model with 9 variables and I am getting the following error message: ‘Error in solve.default(Sigma) : Lapack routine dgesv: system is exactly singular: U[9,9] = 0.
What should I do to deal with it?
Hey Lilian,
Could you illustrate the structure of your data and share the code you have used?
Regards
Joachim
install.packages(“ATE”)
library(ATE)
library(readxl)
YT <- read_excel("ATTQ3.xlsx")
head(YT)
X<- YT[,-c(1:3)]
Ti<- YT$Ti
Y<- YT$Y
fit1<- ATE(Y=Y,Ti=Ti,X=X,ATT=T)
number Y Ti X gender age history type
1 441284199512173… 0 0 0 1 26.4 1 1
2 350628197606226… 0 0 0 1 45.9 7 2
3 440882199710096… 0 0 0 0 24.6 4 2
4 440981198406107… 0 0 0 1 37.9 3 2
5 440821196711111… 0 0 0 1 54.5 9 2
6 230803199809110… 0 0 0 0 23.6 5 2
> fit1<- ATE(Y=Y,Ti=Ti,X=X,ATT=T)
Error in solve.default(H, del.f) :
Lapack routine dgesv: system is exactly singular: U[2,2] = 0
could you help me ? how to deal with it , thanks so much!
Hey Yun,
I have just tried to reproduce your problem, and it seems that the ATE package is not supported anymore (see here).
Do you really have to use this package, or are there maybe better alternatives available?
Looking at your code, it also seems like the columns Ti and X contain only 0. This is another thing I would check in your data.
Regards,
Joachim
Me pueden ayudar?
me salta el error (Error in Inverse(X, tol = sqrt(.Machine$double.eps), …) :
X is numerically singular) y no se como solucionarlo:
Sea
x <- mtcars$disp
X <- cbind(1,x)
# creo la transpuesta de X
Xt <- t(X)
X%*%Xt
# calculo la invrsa
solve(X%*%Xt)
este es mi código.
Hello Maria,
As I understood from the given error, your matrix is singular. Hence you can not take its inverse. See the mathematical explanation here. Also, it will be better if you write in English next time. Google translate might be tricky sometimes. Thank you.
Regards,
Cansu
When I try to perform a multivariate linear analysis of MRM in r, I get the following error message: “Error in solve. default (XX) :
system is computationally singular: reciprocal condition number = 7.10136e-18”
Hello Jialing,
The error message you’re seeing is indicative of multicollinearity in your data. When the matrix X′XX′X (which is derived from your independent variables) is close to singular (or non-invertible), it means that there’s a high degree of multicollinearity among the predictors. The reciprocal condition number being very close to zero is a measure of how close the matrix is to being singular.
Best,
Cansu
I tried the matrix(1:4,2,2) and the solve function worked really well, but then I tried with matrix(1:9,3,3) which for me should work to but I got the same issue than before. Error in solve.default(a) :
Lapack routine dgesv: system is exactly singular: U[3,3] = 0 .. Why?
This is the code that I used:
a <- matrix(1:9,3,3)
a
Ainverse <- solve(a)
Ainverse
Hey Ana,
The error “system is exactly singular: U[3,3] = 0” occurs because the matrix a (constructed with 1:9 in a 3×3 configuration) is singular, meaning it does not have an inverse. This is due to the fact that its determinant is zero, indicating linear dependency among its rows or columns.
I hope this helps!
Joachim