Meeus Great Circle Distance in R (Example)

In this post, I’ll illustrate how to compute the Meeus distance in R programming.

Table of contents:

Let’s get started.

Creation of Example Data

The following data will be used as basement for this R tutorial:

my_points <- matrix(c(81.25798, 73.81277,    # Create longitude/latitude matrix
                      14.91254, 18.18145),
                    nrow = 2)
colnames(my_points) <- c("longitude", "latitude")
rownames(my_points) <- c("pt_1", "pt_2")
my_points                                    # Print longitude/latitude matrix

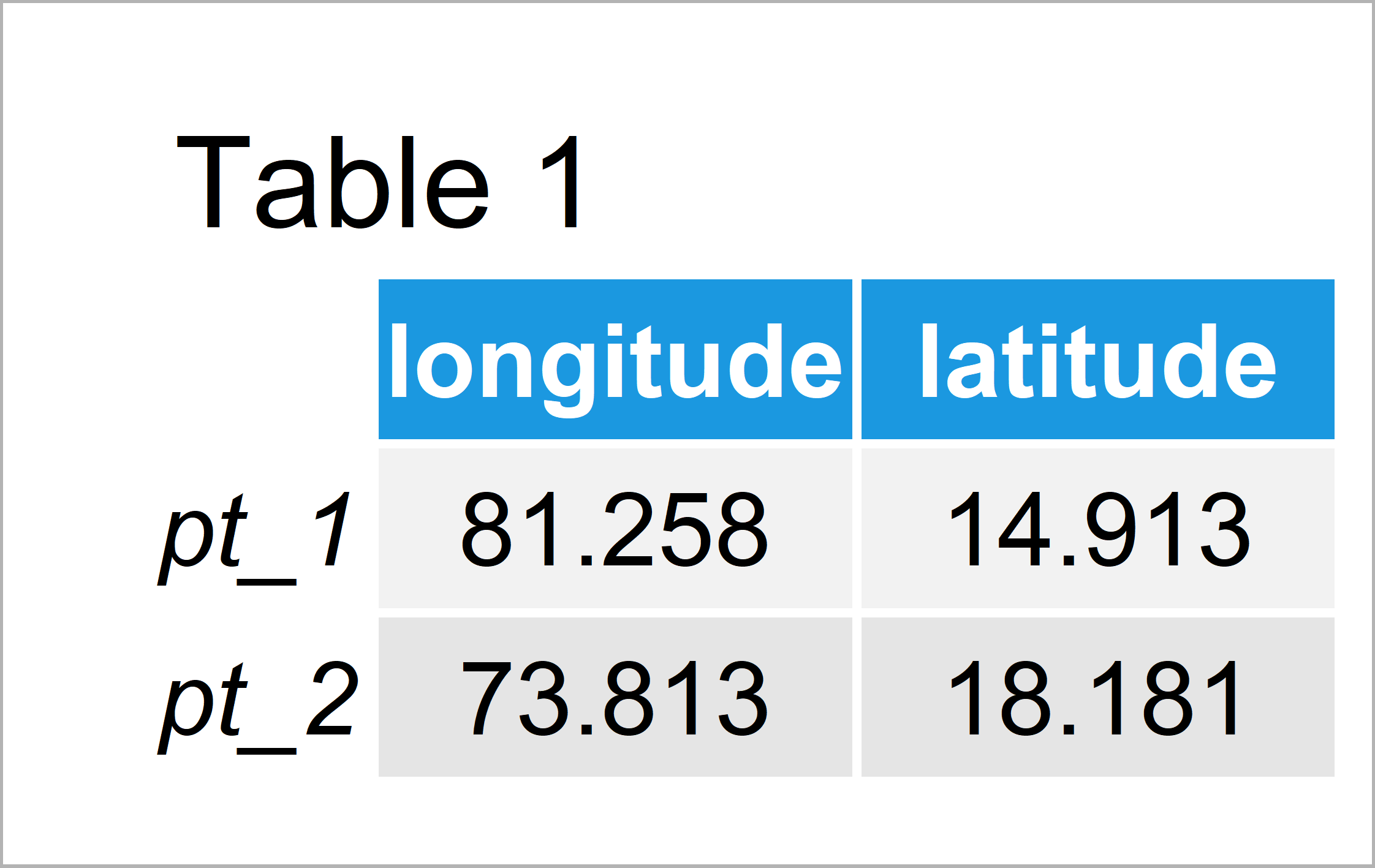
Table 1 shows the structure of our example data – It contains two lines and two variables defining two different geographical points (i.e. longitude and latitude).

Example: Calculate Meeus Great Circle Distance Using distMeeus() Function of geosphere Package

In this example, I’ll show how to calculate the Meeus great circle distance to measure the geospatial distance between our two data points.

For this, we can use the distMeeus function of the geosphere package. First, we need to install and load the geosphere package:

install.packages("geosphere")                # Install & load geosphere package
library("geosphere")

Next, we can apply the distMeeus function to compute the Meeus distance of our two points:

my_dist <- distMeeus(my_points)              # Calculate Meeus distance
my_dist                                      # Print Meeus distance
# [1] 872985.1

The Meeus distance between our two geospatial points is 872985.1.

Video & Further Resources

If you need further information on the topics of this tutorial, you might have a look at the following video which I have published on my YouTube channel. I’m explaining the R codes of this article in the video.

The YouTube video will be added soon.

Furthermore, you may want to read the other tutorials that I have published on my website.

• Haversine Great Circle Distance
• Law of Cosines Great Circle Distance
• Distance Along Rhumb Line
• Vincenty Ellipsoid Great Circle Distance
• Vincenty Sphere Great Circle Distance
• Geospatial Distance Between Two Points
• R Programming Language

In summary: In this R tutorial you have learned how to calculate the Meeus great circle distance. Please let me know in the comments below, if you have further questions.